Função Dispêndio

up:: 062b MOC Teoria do Consumidor

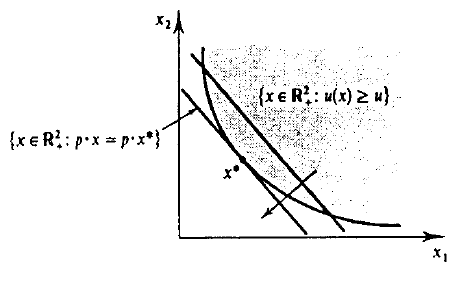
Problema de minimização da função dispêndio. Fonte: MAS-COLLELL et al, p. 58.

A função dispêndio indica a Renda $m$ mínima necessária para se alcançar uma dada Utilidade $\bar{u}$ (dados preços $p$). Ela, portanto, é função dos preços e da utilidade $\bar{u}$ desejada.

Como assumimos que a Cesta Ótima $x^{\ast }$ satisfaz Lei de Walras, temos que a função dispêndio $e(p,\bar{u})$ toma a forma

$$e(p,\bar{u})=⟨p|x^{\ast }⟩\text{ tal que }u(x^{\ast })=\bar{u}$$

Problema de otimização & Lagrangiano associado

Formalmente, o dispêndio vem do problema de otimização

$$\begin{array}{r}\underset{x\ge 0}{\min }⟨p|x⟩\text{ tal que }u(x)=\bar{u}\end{array}$$

Para o problema de otimização, o lagrangiano associado ao problema de multiplicadores de Lagrange é¹

$$\mathcal{L}(x;p,\bar{u})=⟨p|x⟩+\lambda (u(x)-\bar{u})\equiv f(x;p,\bar{u})+\lambda g(x;p,\bar{u})$$

Para fins de conferência: o valor do multiplicador $\lambda$ tem a forma²:

$$\frac{\partial \mathcal{L}}{\partial x}=0⟹\lambda =-\frac{\frac{\partial f}{\partial x}}{\frac{\partial g}{\partial x}}=-\frac{p}{\frac{\partial U}{\partial x}}$$

A otimização de $f(x;p,\bar{u})=⟨p|x⟩$ com relação a $x$, mediante $u(x)=\bar{u}$, assume a forma da função dispêndio quando $x=h^{\ast }$ é a cesta ótima associada a esta otimização³:

$$\begin{array}{rl}e(p,\bar{u})& =f(h^{\ast }(p,\bar{u});p,\bar{u})=⟨p|h^{\ast }⟩\\ & \equiv f^{\ast }(p,\bar{u})\end{array}$$

A cesta $h^{\ast }(p,\bar{u})$ é dita ser a Demanda Hicksiana.

Relações com outros problemas de otimização do consumidor

De acordo com o Envelope Theorem, temos que a derivada da função dispêndio com relação ao preço $p$⁴ pode ser obtido através da derivada do lagrangiano otimizado (avaliado na cesta ótima) com relação ao preço:

$$\frac{\partial e(p,\bar{u})}{\partial p}=\frac{\partial \mathcal{L}(x;p,\bar{u})}{\partial p}{|}_{h^{\ast }(p,\bar{u})}=h^{\ast }(p,\bar{u})$$

Ou seja, A demanda hicksiana é o gradiente da função dispêndio.

Ademais, trivialmente temos — dado $p$ — que, se a Demanda Marshalliana é a cesta ótima num nível de utilidade $\bar{u}$, então a renda certamente tem de ser igual à função dispêndio $e(p,\bar{u})$, a qual é o mínimo nível de renda para se alcançar $\bar{u}$, igualando-se à demanda hicksiana. Portanto, temos a identidade

$$h^{\ast }(p,\bar{u})=x^{\ast }(p,e(p,\bar{u}))$$

O inverso também vale: dado $p$ e certa restrição orçamentária (i.e. renda) $w$, a demanda hicksiana assumida em $p$ e no nível de utilidade da Função de Utilidade Indireta $v(p,w)$ certamente tem de ser igual à demanda walrasiana:

$$x^{\ast }(p,w)=h(p,v(p,w))$$

Propriedades

A função dispêndio é côncava, logo, possui segunda derivada negativa. Isso se reflete no fato de que A Matriz de Slutsky é semi-definida negativa.

---

References

• MAS-COLELL, Andreu et al. Microeconomic theory. New York: Oxford university press, 1995.
• Lab 2.7 Concavity of Expenditure Function (Raphaëlle Chappe)

Footnotes

1. $\mathcal{L}$ também é função de $\lambda$, mas não o denoto para não distrair do problema principal: trata-se da otimização (minimização) no tocante a $x$. ↩

2. Escrevo com derivada parcial para relembrar que $x$ é, na verdade um vetor; portanto, o correto seria escrever $\frac{\partial U}{\partial x_l}$ para cada bem $l$. ↩

3. $x^{\ast }$ é unívoco por assumirmos Preferências do Consumidor que sejam estritamente convexas, localmente não-saciáveis. ↩

4. Formalmente, com relação a algum preço $p_l$ de um bem $l$, de quantidade ótima consumida $x_l$. ↩