Lista 3 Microeconomia - 1.2025

up:: 0x5 MOC Mestrado // 062b MOC Teoria do Consumidor

Exercício 4

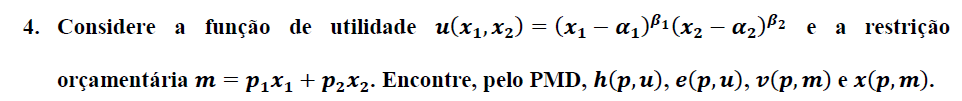
Seja $u(x_1,x_2)=(x_1-{\alpha }_1{)}^{{\beta }_1}(x_2-{\alpha }_2{)}^{{\beta }_2}$ a Função Utilidade, e $m=⟨p|x⟩$ a Restrição Orçamentária.

O problema de minimização de dispêndio é

$$\underset{x}{\min }⟨p|x⟩\mid u(x)=\bar{u}$$

O lagrangiano associado será

$$\mathcal{L}=p_1{x}_1+p_2{x}_2+\lambda \left((x_1-{\alpha }_1{)}^{{\beta }_1}(x_2-{\alpha }_2{)}^{{\beta }_2}-\bar{u}\right)$$

As condições de primeira ordem serão

$$\{\begin{array}{ll}\frac{\partial \mathcal{L}}{\partial x_1}=0⟹p_1& =-\lambda {\beta }_1(x_1-{\alpha }_1{)}^{{\beta }_1-1}(x_2-{\alpha }_2{)}^{{\beta }_2}\\ \frac{\partial \mathcal{L}}{\partial x_2}=0⟹p_2& =-\lambda {\beta }_2(x_1-{\alpha }_1{)}^{{\beta }_1}(x_2-{\alpha }_2{)}^{{\beta }_2-1}\\ \frac{\partial \mathcal{L}}{\partial \lambda }=0⟹\bar{u}& =(x_1-{\alpha }_1{)}^{{\beta }_1}(x_2-{\alpha }_2{)}^{{\beta }_2}\end{array}$$

Dividindo as primeiras duas equações, temos

$$\begin{array}{rl}\frac{p_1}{p_2}& =\frac{{\beta }_1}{{\beta }_2}\frac{x_2-{\alpha }_2}{x_1-{\alpha }_1}\\ \therefore x_2-{\alpha }_2& =\frac{{\beta }_2}{p_2}\frac{p_1}{{\beta }_1}(x_1-{\alpha }_1)\end{array}$$

Pela restrição de utilidade, temos

$$\bar{u}={\left(\frac{{\beta }_2}{p_2}\frac{p_1}{{\beta }_1}\right)}^{{\beta }_2}(x_1-{\alpha }_1{)}^{{\beta }_1+{\beta }_2}$$

Portanto, isolando para $x_1$ — e, portanto, para $x_2$ —, obtém-se as Demandas Hicksianas

$$\{\begin{array}{l}{x}_1^{\ast }=:h_1={\alpha }_1+{\bar{u}}^{\frac{1}{{\beta }_1+{\beta }_2}}{\left(\frac{{\beta }_1}{p_1}\frac{p_2}{{\beta }_2}\right)}^{\frac{{\beta }_2}{{\beta }_1+{\beta }_2}}\\ x_2^{\ast }=:h_2={\alpha }_2+{\bar{u}}^{\frac{1}{{\beta }_1+{\beta }_2}}{\left(\frac{{\beta }_2}{p_2}\frac{p_1}{{\beta }_1}\right)}^{\frac{{\beta }_1}{{\beta }_1+{\beta }_2}}\end{array}$$

A Função Dispêndio é

$$e(p,\bar{u})=⟨p|h⟩=p_1\left({\alpha }_1+{\bar{u}}^{\frac{1}{{\beta }_1+{\beta }_2}}{\left(\frac{{\beta }_1}{p_1}\frac{p_2}{{\beta }_2}\right)}^{\frac{{\beta }_2}{{\beta }_1+{\beta }_2}}\right)+p_2\left({\alpha }_2+{\bar{u}}^{\frac{1}{{\beta }_1+{\beta }_2}}{\left(\frac{{\beta }_2}{p_2}\frac{p_1}{{\beta }_1}\right)}^{\frac{{\beta }_1}{{\beta }_1+{\beta }_2}}\right)$$

Tomando o dispêndio como sendo algum valor $w$, e isolando em termos de $\bar{u}$, temos a Função de Utilidade Indireta $v(p,w):=\bar{u}$. Deixado como exercício para o leitor corajoso.¹ Encontre também as demandas marshallianas while you’re at it.

Exercício 6

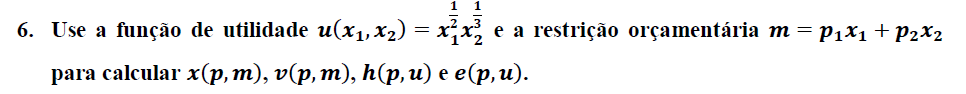
A função utilidade é uma Função de Cobb-Douglas $u(x_1,x_2)=x_1^{1/2}{x}_2^{1/3}$, com restrição orçamentária $m=⟨p|x⟩$.

O problema de maximização de utilidade tem as condições de primeira ordem:

$$\{\begin{array}{l}\frac{1}{2}{x}_1^{-1/2}{x}_2^{1/3}=-\lambda p_1\\ \frac{1}{3}{x}_1^{1/2}{x}_2^{-2/3}=-\lambda p_2\end{array}$$

Dividindo a primeira pela segunda, temos

$$\begin{array}{r}\frac{3}{2}{x}_1^{-1}{x}_2^1=\frac{p_1}{p_2}\\ \therefore x_2=\frac{p_1}{p_2}\frac{2}{3}{x}_1\end{array}$$

Substituindo na restrição orçamentária, temos as Demandas Marshallianas:

$$\begin{array}{r}{p}_1{x}_1+p_2\frac{p_1}{p_2}\frac{2}{3}{x}_1=m\\ \therefore \{\begin{array}{l}{x}_1=\frac{3}{5}\frac{m}{p_1}\\ x_2=\frac{2}{5}\frac{m}{p_2}\end{array}\end{array}$$

Perceba-se que as frações são os pesos que esses bens possuem numa função Cobb-Douglas normalizada:²

$$\begin{array}{rl}\frac{1}{2}+\frac{1}{3}& =1\\ =\frac{3}{5}+\frac{2}{5}& \end{array}$$

Através dela, podemos obter a Função de Utilidade Indireta, utilidade obtida nesta cesta ótima:

$$\begin{array}{rl}v(p,w)& =u(x^{\ast })={\left(\frac{3}{5}\frac{m}{p_1}\right)}^{1/2}{\left(\frac{2}{5}\frac{m}{p_2}\right)}^{1/3}\\ & ={\left(\frac{m}{5}\right)}^{5/6}{\left(\frac{3}{p_1}\right)}^{1/2}{\left(\frac{2}{p_2}\right)}^{1/3}\\ & ={\left(\frac{m}{5}\right)}^{5/6}{\left(3p_1^{-1}\right)}^{1/2}{\left(2p_2^{-1}\right)}^{1/3}\end{array}$$

Fazendo com que $v(p,w)=\bar{u}$, e isolando em função de $e(p,\bar{u}):=m$, temos a Função Dispêndio

$$e(p,\bar{u})=5{\left(\frac{p_1}{3}\right)}^{3/5}{\left(\frac{p_2}{2}\right)}^{2/5}{\bar{u}}^{6/5}$$

Como A demanda condicional de fatores de produção é o gradiente da função custo, temos que a Demanda Hicksiana é

$$\{\begin{array}{l}{h}_1(p,\bar{u})=\frac{\partial e}{\partial p_1}={\left(\frac{p_1}{3}\right)}^{-2/5}{\left(\frac{p_2}{2}\right)}^{2/5}{\bar{u}}^{6/5}\\ h_2(p,\bar{u})=\frac{\partial e}{\partial p_2}={\left(\frac{p_1}{3}\right)}^{3/5}{\left(\frac{p_2}{2}\right)}^{-3/5}{\bar{u}}^{6/5}\end{array}$$

---

References

• MAS-COLELL, Andreu; WHINSTON, Michael Dennis; GREEN, Jerry R. Microeconomic theory. New York: Oxford University Press, 1995.

Footnotes

1. A vida é curta demais para resolver um problema imbecil como esse! ↩

2. Funções monotônicas preservam curvas de indiferença. A função monotônica que levaria a função dada pelo exercício a essa normalizada seria a função potência $f(z)=z^{6/5}$: $x^{1/2}\mapsto x^{3/5}$; $x^{1/3}\mapsto x^{2/5}$. ↩