Simple Graph

up:: 041 MOC Graph Theory

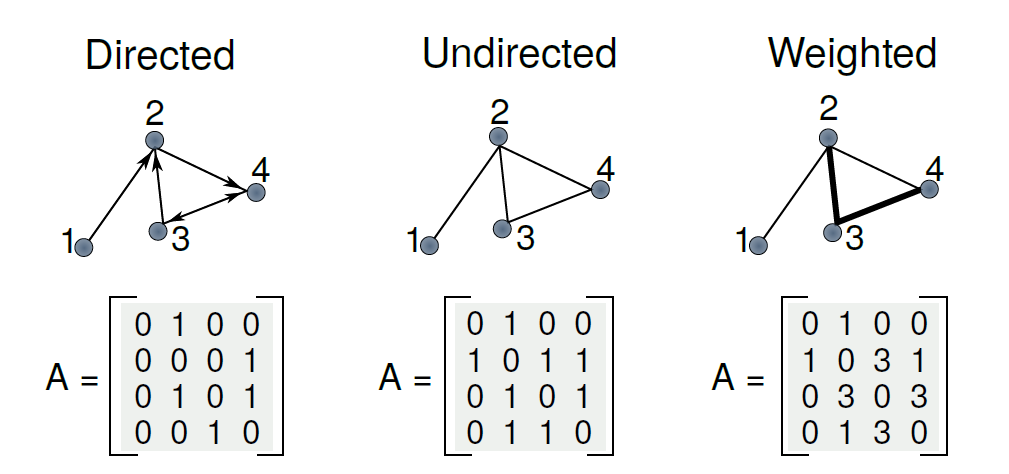
A simple graph is a double , where is a set of nodes, and is the set of edges between nodes in .

More generally, one can think of as a subset of , that is, edges have sources and targets that are subsets of .

For the case of simple graphs, all edges are composed of doubles of singleton sets of nodes, i.e. one-to-one relations between nodes. Thus, one can unambiguously define their Adjacency Matrix.

Other types of graphs

Other types of graphs can have different compositions of elements of , for instance Hypergraphs, which can encode more complex relationships between nodes, such as one-to-many (e.g. lectures), many-to-one (e.g. protests) and many-to-many (e.g. complex chemical reactions, I guess?) relationships.

---

References

• Casas, Alberto Aleta. “Networks, epidemics and collective behavior: from physics to data science”. PhD Thesis, Universidad de Zaragoza, 2019. https://dialnet.unirioja.es/servlet/tesis?codigo=300533.