Node Betweenness

up:: 041 MOC Graph Theory

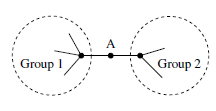
Example of node with high betweenness but low degree.

“A point is considered to be central here to the degree that it falls between other points on their shortest or geodesic communication paths. A point falling between two others can facilitate, block, distort or falsify communication between the two; it can more or less completely control their communication. But if it falls on some but not all of the geodesics connecting a pair of points, its potential for control is more limited.” (Freeman, 1977; my emphasis)

The betweeness of a node (in a Simple Graph ) is a measure of, given Shortest Path Distances between all nodes , how “likely” it is to have to pass through . It is a measure of ‘s centrality.

It’s given by

This normalization factor is the amount of possible shortest paths from to through .¹

The maximal case in which is central is a [graph component which is a] Star Graph where is the central node.

---

References

• FREEMAN, L. C. A Set of Measures of Centrality Based on Betweenness. Sociometry, v. 40, n. 1, p. 35–41, 1977.
• NEWMAN, Mark. Networks. Oxford University Press, 2018.

Footnotes

1. Taking into account only nodes which are reachable in the network, and disconsidering those that are in separate components. ↩