Kuramoto Model

up:: 041 MOC Graph Theory

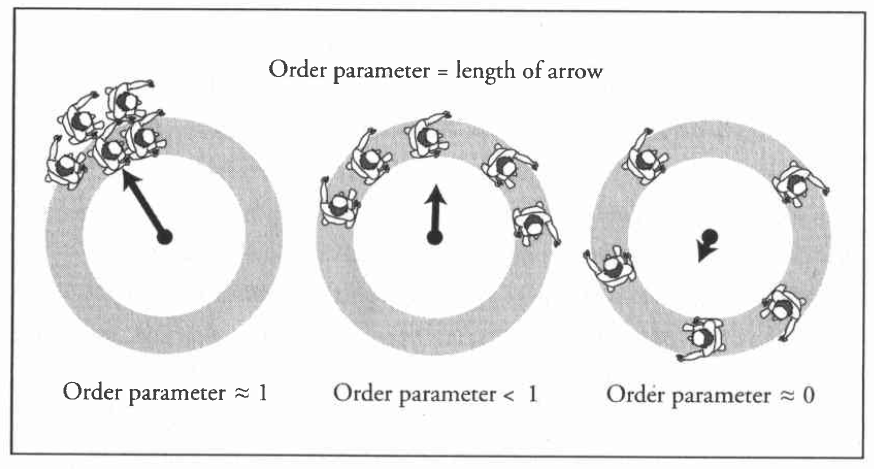
(From Strogatz’s book “Sync: How order emerges from chaos in the universe, nature, and daily life”)

In 1975, Kuramoto proposed a model for the synchronization of coupled oscillators, as a solution to Winfree’s Model of Synchronization, of the form

$$\dot{{\theta }_i}={\omega }_i+\frac{K}{N}\sum _{j=1}^N\sin ({\theta }_j-{\theta }_i)$$

in which all oscillators interact with each other to some extent¹, with coupling strength $K>0$.

One can write the Kuramoto Model Order Parameter as

$$R{e}^{i\psi }=\sum _{i=1}^N{e}^{i{\theta }_i}$$

i.e. the average (complex) phase of the system, with which one can rewrite the Kuramoto model as

$$\dot{{\theta }_i}={\omega }_i+\frac{KR}{N}\sin (\psi -{\theta }_i)$$

This shows the model’s explicit dependence to a Mean Field with which all other oscillators align. The oscillators are all coupled to each other, but it appears that they’re individually only coupled to some mean field which influences them, and which, in turn, is influenced by them, and so on.

Assumptions of the Kuramoto model

The Kuramoto model assumes the following:

1. All oscillators are coupled with same coupling strength (originally, $\frac{K}{N}$);
2. $N\to \infty$ (number of oscillators);
3. The order parameter $R$ tends to a constant $R_{\infty }(K)$ as $t\to \infty$ and $N\to \infty$

Phase transition

The Kuramoto model has a second-order phase transition.

---

References

• KURAMOTO, Y. Self-entrainment of a population of coupled non-linear oscillators. (H. Araki, Ed.) International Symposium on Mathematical Problems in Theoretical Physics. Anais…Berlin, Heidelberg: Springer, 1975.
• STROGATZ, S. H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. 3. ed. CRC Press, 2019.
• 2011 Simons Lectures - Steven Strogatz, Coupled Oscillators That Synchronize Themselves - YouTube
• Complexity Explorables | Ride my Kuramotocycle!

Footnotes

1. I.e. they relate through a fully-connected Simple Graph. ↩