The Kuramoto model has a second-order phase transition

up:: Kuramoto Model

(Strogatz)

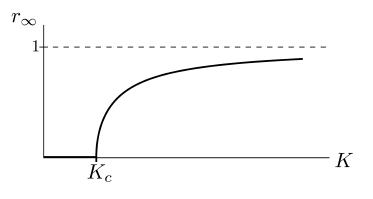
The Kuramoto model has a Second-Order Phase Transition with respect to its coupling parameter .

This means that, below some critical coupling threshold , there can be no synchronization (), no matter how long one waits or how many oscillators there are.

Only past this threshold can synchronization begin to happen (asymptotically in and ).

Derivation of threshold

One can find this critical threshold solving a self-consistent equation for the Kuramoto Model Order Parameter , of the form

By making ¹, one finds the critical coupling

Derivation of second-order transition

Expanding around up to second order², and since , we have

---

References

• KURAMOTO, Y. Self-entrainment of a population of coupled non-linear oscillators. (H. Araki, Ed.), 1975.
• STROGATZ, S. H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. 3. ed. CRC Press, 2019.
• 2011 Simons Lectures - Steven Strogatz, Coupled Oscillators That Synchronize Themselves - YouTube

Footnotes

1. And implicitly assuming continuity of . ↩

2. Assuming follows a Lorentzian distribution (), as (Kuramoto, 1975). ↩