Jaccard Similarity

up:: 041 MOC Graph Theory

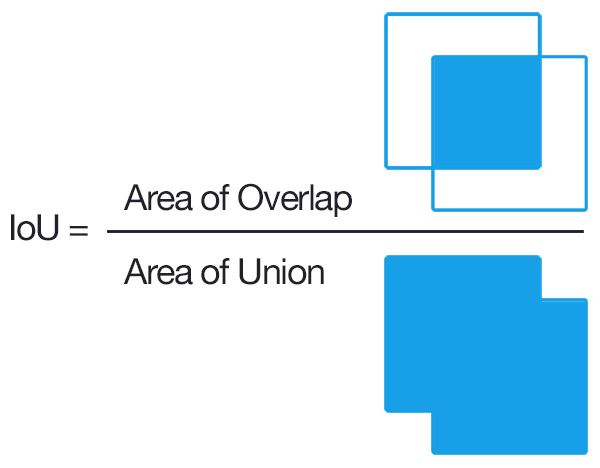
Intersection over Union, visually. Source: Wikipedia.

Given a Simple Graph with Adjacency Matrix and nodes , then their Jaccard similarity is the fraction of common neighbors out of the union of all of their neighbors.

One can calculate the Jaccard similarity between and as

where is the amount of common neighbors of and , i.e. the amount of nodes through which can go to and vice-versa¹, or the number of 2-paths from to .

Note that this formula could be rewritten as

I.e. it is the fraction of common neighbors (intersection) out of all of both’s neighbors (union). This measure is also used in Computer Vision, under the guise of “Intersection over Union”.

---

Note that, when compared with Cosine Similarity, it can be proven that Jaccard Similarity is a lower-bound for Cosine Similarity: for any (non-disjoint) nodes . That is, cosine similarity is a more “loose” measure of similarity than Jaccard similarity.

---

References

• NEWMAN, Mark. Networks. Oxford University Press, 2018.
• Jaccard index - Wikipedia

Footnotes

1. Note this makes sense only for undirected networks. ↩