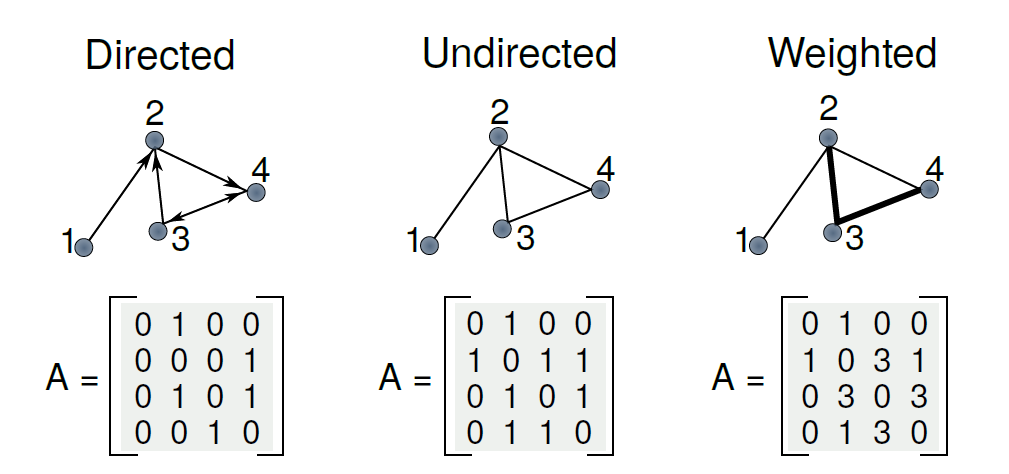
Given a graph $G$ , one can describe its nodes’ interrelations through $G$ ‘s adjacency matrix $A$ .

Outward-Arrows Convention

I’ll focus on the convention

A_{ij} \equiv A_{i \to j}

that is, $A_{ij}$ refers to an “arrow” from $i$ to $j$ .

Properties

Given this convention above, one can define each node’s Node Degree (for undirected networks), and their In Degree and Out Degree (for directed networks)
The adjacency matrix description of a graph $G$ is equivalent to its description via a Laplacian Matrix ─ for Simple Graphs, at least
For Multi-layer graphs, the adjacency matrix of the ensemble of graphs is the direct sum of the individual adjacency matrices of the graphs, plus an intra-layer matrix

Casas, Alberto Aleta. “Networks, epidemics and collective behavior: from physics to data science”. PhD Thesis, Universidad de Zaragoza, 2019. https://dialnet.unirioja.es/servlet/tesis?codigo=300533.