Modelo de Solow

up:: 061 MOC Macroeconomia

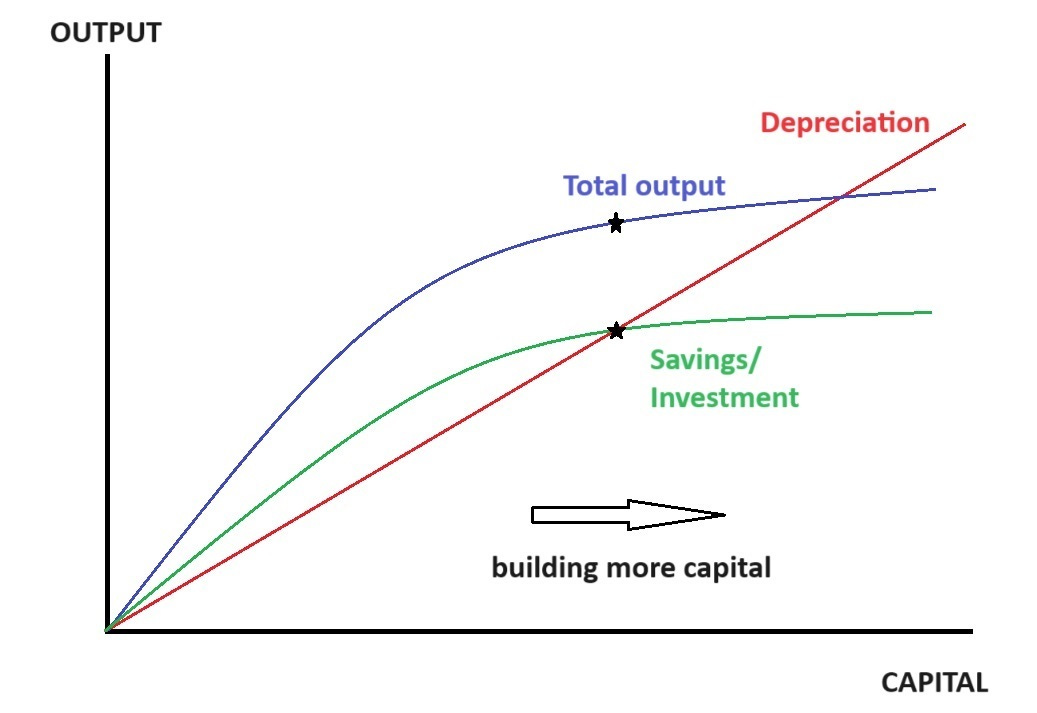
Fonte: Noahpinion.

O modelo de Solow é um modelo sobre o crescimento econômico lato sensu de uma economia.

Definição matemática

Dada uma Função Produção que descreve o Produto Agregado em termos do Capital e da Força de Trabalho , supõe-se que ela tenha retornos constantes em escala:

Ou seja, supõe-se que a economia seja desenvolvida o suficiente para conseguir um retorno proporcional ao capital a mais investido na produção.

Além disso, empregam-se as seguintes equações dinâmicas:

onde é a taxa de Depreciação, é o Investimento no tempo e é a taxa de Poupança.

Além disso, podemos supor que

onde representa o nível de tecnologia da economia¹.

Modelo de Solow com Força de Trabalho constante/exógena

Supondo constante, podemos trabalhar com as variáveis per capita:

Analisando o crescimento de capital per capita, temos

Como temos que , temos

onde é o crescimento (growth) percentual de no tempo .

Steady states

Buscando um estado estável neste modelo, fazemos . Disso temos²

que são as variáveis de equilíbrio per capita. Note-se que, como é exógeno, as variáveis base também alcançarão um equilíbrio (só multiplicar as respectivas variáveis per capita por ).

Ou seja, note-se que

• mudanças permanentes na poupança têm efeitos diretamente proporcionais em todas variáveis – menos no consumo
• mudanças permanentes no nível tecnológico têm efeitos diretamente proporcionais em todas variáveis
• mudanças permanentes na depreciação têm efeitos inversamente proporcionais em todas variáveis

O Consumo, em particular, é afetado inversamente pela poupança do que os investimentos são. Portanto, precisa ser considerado diferentemente. Busquemos então algum que maximize o consumo de equilíbrio. Isso é equivalente a buscar o máximo consumo no tocante ao capital de equilíbrio:

Este ponto é um máximo, devido à hipótese que a função de produção possui retornos marginais decrescentes, i.e.

Portanto, através do investimento, temos que

é a taxa de poupança necessária para maximizar o consumo. Essa é a chamada regra de ouro do modelo de Solow.

Equilíbrio com produção Cobb-Douglas

Supondo, por exemplo, uma Função de Cobb-Douglas de produção, temos

Dessa forma, teríamos

Modelo de Solow com Força de Trabalho variável/endógena

Supomos, além das equações prévias, uma equação dinâmica da variável :

onde é a taxa de crescimento da força de trabalho (exógena). Note-se que isso é equivalente a dizer que

As variáveis per capita agora são baseadas em :

Note-se que o crescimento do capital per capita muda:

onde usa-se a aproximação³ , e aproximações de primeira ordem em ⁴.

Fazendo , temos⁵

Steady states

No equilíbrio, o capital per capita é constante. Disso obtemos

A regra de ouro tem como taxa de poupança ótima

Crescimento de variáveis base

Enquanto as variáveis per capita chegam a um equilíbrio, as variáveis base têm crescimento não-nulo. Note-se que está crescendo geometricamente: o capital per capita chega a uma constante, pois o capital em si passa a crescer na mesma taxa que a taxa de crescimento da força de trabalho. Matematicamente:

Para todas as variáveis que chegam a um equilíbrio per capita, temos que elas crescerão na proporção da força de trabalho em suas variáveis base: seja uma variável cujo per capita chega a um equilíbrio conforme . Então temos

Ou seja, neste modelo, o crescimento econômico em geral cresce na mesma proporção que o aumento da força de trabalho. Este é o chamado “caminho de crescimento sustentado” (balanced growth path).

---

References

• Solow Growth Model - YouTube
• What the Solow Model can teach us about China (Noahpinion)
• solow_SL.pdf
• macroeconomics - Three types of Neutral technological Change - Economics Stack Exchange

Footnotes

1. Supondo que a função produção tenha retornos constantes em escala, esse sai como fator de ambos e , sendo uma nível tecnológico médio geral da economia. ↩

2. Note-se que, neste estado de equilíbrio, temos que o investimento é exatamente igual à depreciação, nem mais, nem menos. Quando se chega a este estado, investir mais acaba sendo detrimental, devido à força de trabalho constante “ficar para trás”. ↩

3. Quando , mas duvido que economistas tenham isso em mente. ↩

4. I.e. desconsiderando termos etc. De novo, isso vale quando , e, de novo, vide acima. ↩

5. De novo, assumindo , ou ao menos que . ↩