up:: Category
A functor is essentially a “translation” of what happens inside a category into another category .
Given categories , a functor is a morphism which preserves their structure:
- All objects in are mapped to objects in
- All morphisms in are mapped to morphisms in
- The functor acts as a Homomorphism of sorts, preserving the algebraic composition of morphisms:
Properties
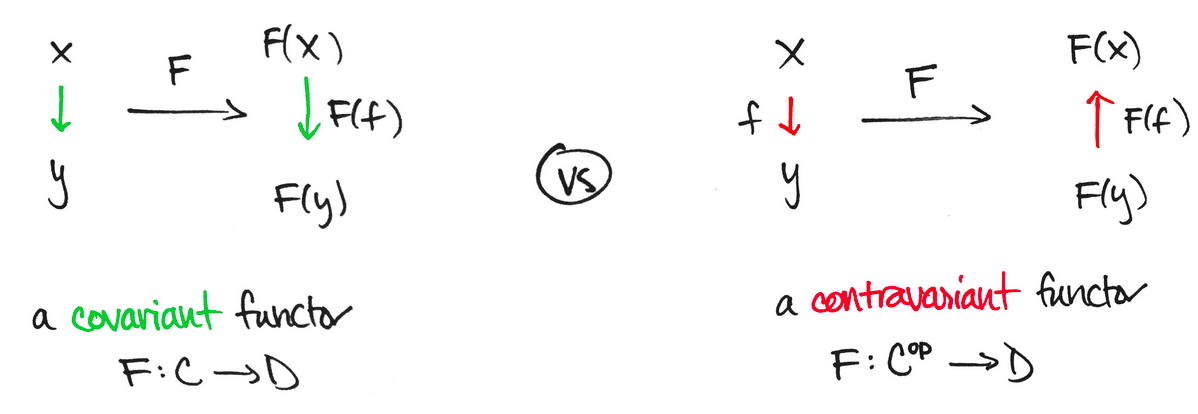
Functors can either be covariant or Contravariant, depending on whether its action “flips” morphisms in the target category or not.
Examples
- A Group Homomorphism between Groups can be seen as a functor between their respective single-element categories
- Group Actions can be seen as functors from a groupoid with a single element onto another category
References
Drawing
{
"type": "excalidraw",
"version": 2,
"source": "https://github.com/zsviczian/obsidian-excalidraw-plugin/releases/tag/2.1.6",
"elements": [
{
"type": "freedraw",
"version": 5,
"versionNonce": 1971155780,
"isDeleted": false,
"id": "N-aDlwFosXSiU5hN_2gYE",
"fillStyle": "hachure",
"strokeWidth": 1,
"strokeStyle": "solid",
"roughness": 1,
"opacity": 100,
"angle": 0,
"x": -146.2495231628418,
"y": -90.49861907958984,
"strokeColor": "#1e1e1e",
"backgroundColor": "transparent",
"width": 0.0001,
"height": 0.0001,
"seed": 2008154620,
"groupIds": [],
"frameId": null,
"roundness": null,
"boundElements": [],
"updated": 1691265040623,
"link": null,
"locked": false,
"points": [
[
0,
0
],
[
0.0001,
0.0001
]
],
"lastCommittedPoint": null,
"simulatePressure": true,
"pressures": []
},
{
"type": "freedraw",
"version": 5,
"versionNonce": 1102664444,
"isDeleted": false,
"id": "vGgn_p_coJ42sJprxt2Kw",
"fillStyle": "hachure",
"strokeWidth": 1,
"strokeStyle": "solid",
"roughness": 1,
"opacity": 100,
"angle": 0,
"x": -142.19230270385742,
"y": 70.2680892944336,
"strokeColor": "#1e1e1e",
"backgroundColor": "transparent",
"width": 0.0001,
"height": 0.0001,
"seed": 326243140,
"groupIds": [],
"frameId": null,
"roundness": null,
"boundElements": [],
"updated": 1691265040623,
"link": null,
"locked": false,
"points": [
[
0,
0
],
[
0.0001,
0.0001
]
],
"lastCommittedPoint": null,
"simulatePressure": true,
"pressures": []
},
{
"type": "freedraw",
"version": 80,
"versionNonce": 1333160644,
"isDeleted": false,
"id": "jROwmI2Mw_wjRJO_74Doq",
"fillStyle": "hachure",
"strokeWidth": 1,
"strokeStyle": "solid",
"roughness": 1,
"opacity": 100,
"angle": 0,
"x": 36.32472610473633,
"y": -96.07727813720703,
"strokeColor": "#1e1e1e",
"backgroundColor": "transparent",
"width": 0.0001,
"height": 0.0001,
"seed": 788984700,
"groupIds": [],
"frameId": null,
"roundness": null,
"boundElements": [],
"updated": 1691265040623,
"link": null,
"locked": false,
"points": [
[
0,
0
],
[
0.0001,
0.0001
]
],
"lastCommittedPoint": null,
"simulatePressure": true,
"pressures": []
},
{
"type": "freedraw",
"version": 79,
"versionNonce": 1502450556,
"isDeleted": false,
"id": "5t4tezz5gjc_oLZQy7V8M",
"fillStyle": "hachure",
"strokeWidth": 1,
"strokeStyle": "solid",
"roughness": 1,
"opacity": 100,
"angle": 0,
"x": 41.90333938598633,
"y": 72.2966537475586,
"strokeColor": "#1e1e1e",
"backgroundColor": "transparent",
"width": 0.0001,
"height": 0.0001,
"seed": 1593767676,
"groupIds": [],
"frameId": null,
"roundness": null,
"boundElements": [],
"updated": 1691265040623,
"link": null,
"locked": false,
"points": [
[
0,
0
],
[
0.0001,
0.0001
]
],
"lastCommittedPoint": null,
"simulatePressure": true,
"pressures": []
},
{
"type": "arrow",
"version": 48,
"versionNonce": 1295208900,
"isDeleted": false,
"id": "ufLvTBiY0OWPi_wxLaPyR",
"fillStyle": "hachure",
"strokeWidth": 1,
"strokeStyle": "solid",
"roughness": 0,
"opacity": 100,
"angle": 0,
"x": -147.2638053894043,
"y": -91.00577545166016,
"strokeColor": "#1e1e1e",
"backgroundColor": "transparent",
"width": 3.042877197265625,
"height": 160.25955200195312,
"seed": 462429124,
"groupIds": [],
"frameId": null,
"roundness": {
"type": 2
},
"boundElements": [],
"updated": 1691265059960,
"link": null,
"locked": false,
"startBinding": {
"elementId": "xwfp0FVV",
"focus": -2.2017025258620735,
"gap": 9.75030517578125
},
"endBinding": {
"elementId": "ySjONQgN",
"focus": 2.0606293692588444,
"gap": 7.707305908203125
},
"lastCommittedPoint": null,
"startArrowhead": null,
"endArrowhead": "arrow",
"points": [
[
0,
0
],
[
3.042877197265625,
160.25955200195312
]
]
},
{
"type": "arrow",
"version": 131,
"versionNonce": 890459772,
"isDeleted": false,
"id": "uMUYXu6UL8g9FFdjKx1-h",
"fillStyle": "hachure",
"strokeWidth": 1,
"strokeStyle": "solid",
"roughness": 0,
"opacity": 100,
"angle": 0,
"x": 36.83186721801758,
"y": -97.09159088134766,
"strokeColor": "#1e1e1e",
"backgroundColor": "transparent",
"width": 5.07147216796875,
"height": 169.38824462890625,
"seed": 373801724,
"groupIds": [],
"frameId": null,
"roundness": {
"type": 2
},
"boundElements": [],
"updated": 1691265094905,
"link": null,
"locked": false,
"startBinding": {
"elementId": "GP57pZUX",
"focus": 1.2203981897314486,
"gap": 4.30029296875
},
"endBinding": {
"elementId": "Ms8Qbmxl",
"focus": -1.43989993384693,
"gap": 7.32891845703125
},
"lastCommittedPoint": null,
"startArrowhead": null,
"endArrowhead": "arrow",
"points": [
[
0,
0
],
[
5.07147216796875,
169.38824462890625
]
]
},
{
"type": "rectangle",
"version": 84,
"versionNonce": 1092979140,
"isDeleted": false,
"id": "pmogieRAkpXk3XWF2Q0Ee",
"fillStyle": "hachure",
"strokeWidth": 1,
"strokeStyle": "solid",
"roughness": 0,
"opacity": 100,
"angle": 0,
"x": -191.89304733276367,
"y": -103.68453216552734,
"strokeColor": "#1e1e1e",
"backgroundColor": "transparent",
"width": 93.315673828125,
"height": 197.78868103027344,
"seed": 396237948,
"groupIds": [],
"frameId": null,
"roundness": {
"type": 3
},
"boundElements": [],
"updated": 1691265040623,
"link": null,
"locked": false
},
{
"type": "rectangle",
"version": 145,
"versionNonce": 621333060,
"isDeleted": false,
"id": "3HcAgVEDjmzbWv8__JUJs",
"fillStyle": "hachure",
"strokeWidth": 1,
"strokeStyle": "solid",
"roughness": 0,
"opacity": 100,
"angle": 0,
"x": -7.797435760498047,
"y": -105.20597076416016,
"strokeColor": "#1e1e1e",
"backgroundColor": "transparent",
"width": 99.40145874023439,
"height": 198.29580688476562,
"seed": 819134844,
"groupIds": [],
"frameId": null,
"roundness": {
"type": 3
},
"boundElements": [],
"updated": 1691265103552,
"link": null,
"locked": false
},
{
"type": "image",
"version": 79,
"versionNonce": 1255649604,
"isDeleted": false,
"id": "Ud3FRrUz",
"fillStyle": "hachure",
"strokeWidth": 1,
"strokeStyle": "solid",
"roughness": 1,
"opacity": 100,
"angle": 0,
"x": -152.48676554816737,
"y": 102.63003419287723,
"strokeColor": "#000000",
"backgroundColor": "transparent",
"width": 19.574643462057406,
"height": 12.36293271287836,
"seed": 84669,
"groupIds": [],
"frameId": null,
"roundness": null,
"boundElements": [],
"updated": 1691265040623,
"link": null,
"locked": false,
"status": "pending",
"fileId": "289e342afb7b3299316494a64883d7b99c0c7ed5",
"scale": [
1,
1
]
},
{
"type": "image",
"version": 82,
"versionNonce": 702235516,
"isDeleted": false,
"id": "oEeeavVl",
"fillStyle": "hachure",
"strokeWidth": 1,
"strokeStyle": "solid",
"roughness": 1,
"opacity": 100,
"angle": 0,
"x": 37.48903274536133,
"y": 103.81868743896484,
"strokeColor": "#000000",
"backgroundColor": "transparent",
"width": 21,
"height": 11,
"seed": 65166,
"groupIds": [],
"frameId": null,
"roundness": null,
"boundElements": [],
"updated": 1691265106458,
"link": null,
"locked": false,
"status": "pending",
"fileId": "ce922c3c8eddbdb2cb188b611839d97cd9ae847b",
"scale": [
1,
1
]
},
{
"type": "image",
"version": 46,
"versionNonce": 159417540,
"isDeleted": false,
"id": "ySjONQgN",
"fillStyle": "hachure",
"strokeWidth": 1,
"strokeStyle": "solid",
"roughness": 1,
"opacity": 100,
"angle": 0,
"x": -166.2394956504811,
"y": 60.97344730219244,
"strokeColor": "#000000",
"backgroundColor": "transparent",
"width": 14.622523100278618,
"height": 11.489125293076057,
"seed": 54301,
"groupIds": [],
"frameId": null,
"roundness": null,
"boundElements": [
{
"id": "ufLvTBiY0OWPi_wxLaPyR",
"type": "arrow"
},
{
"id": "zzDvrTfTjVv1EtK9IqXXJ",
"type": "arrow"
}
],
"updated": 1691265077615,
"link": null,
"locked": false,
"status": "pending",
"fileId": "30fad90474670bf0e950c559425ac13ca31b629e",
"scale": [
1,
1
]
},
{
"type": "image",
"version": 46,
"versionNonce": 305978692,
"isDeleted": false,
"id": "xwfp0FVV",
"fillStyle": "hachure",
"strokeWidth": 1,
"strokeStyle": "solid",
"roughness": 1,
"opacity": 100,
"angle": 0,
"x": -173.01411056518555,
"y": -93.99861907958984,
"strokeColor": "#000000",
"backgroundColor": "transparent",
"width": 16,
"height": 7,
"seed": 98272,
"groupIds": [],
"frameId": null,
"roundness": null,
"boundElements": [
{
"id": "ufLvTBiY0OWPi_wxLaPyR",
"type": "arrow"
},
{
"id": "G2qwQAt_V_swf9_N1wAG7",
"type": "arrow"
}
],
"updated": 1691265070230,
"link": null,
"locked": false,
"status": "pending",
"fileId": "76fafa5976f1f375b34db647150fdeaded57ea2a",
"scale": [
1,
1
]
},
{
"type": "image",
"version": 56,
"versionNonce": 1595399676,
"isDeleted": false,
"id": "umhz7cma",
"fillStyle": "hachure",
"strokeWidth": 1,
"strokeStyle": "solid",
"roughness": 1,
"opacity": 100,
"angle": 0,
"x": -176.56415939331055,
"y": -20.40460968017578,
"strokeColor": "#000000",
"backgroundColor": "transparent",
"width": 16,
"height": 15,
"seed": 67861,
"groupIds": [],
"frameId": null,
"roundness": null,
"boundElements": [
{
"id": "91jbTV-L3y2-cSdbHohNC",
"type": "arrow"
}
],
"updated": 1691265083391,
"link": null,
"locked": false,
"status": "pending",
"fileId": "8956dc5f117d07dff9cee88934674e3bf3f8432c",
"scale": [
1,
1
]
},
{
"type": "arrow",
"version": 57,
"versionNonce": 2074405444,
"isDeleted": false,
"id": "G2qwQAt_V_swf9_N1wAG7",
"fillStyle": "hachure",
"strokeWidth": 2,
"strokeStyle": "solid",
"roughness": 0,
"opacity": 100,
"angle": 0,
"x": -144.72806930541992,
"y": -89.99146270751953,
"strokeColor": "#1971c2",
"backgroundColor": "transparent",
"width": 179.53125,
"height": 6.0858154296875,
"seed": 182065916,
"groupIds": [],
"frameId": null,
"roundness": {
"type": 2
},
"boundElements": [],
"updated": 1691265090248,
"link": null,
"locked": false,
"startBinding": {
"elementId": "xwfp0FVV",
"focus": 0.3168286239149397,
"gap": 12.286041259765625
},
"endBinding": {
"elementId": "GP57pZUX",
"focus": 0.8694017741105197,
"gap": 6.3289794921875
},
"lastCommittedPoint": null,
"startArrowhead": null,
"endArrowhead": "arrow",
"points": [
[
0,
0
],
[
179.53125,
-6.0858154296875
]
]
},
{
"type": "arrow",
"version": 64,
"versionNonce": 1775970044,
"isDeleted": false,
"id": "zzDvrTfTjVv1EtK9IqXXJ",
"fillStyle": "hachure",
"strokeWidth": 2,
"strokeStyle": "solid",
"roughness": 0,
"opacity": 100,
"angle": 0,
"x": -142.69944381713867,
"y": 70.2680892944336,
"strokeColor": "#1971c2",
"backgroundColor": "transparent",
"width": 182.0670166015625,
"height": 2.028594970703125,
"seed": 5966204,
"groupIds": [],
"frameId": null,
"roundness": {
"type": 2
},
"boundElements": [],
"updated": 1691265094905,
"link": null,
"locked": false,
"startBinding": {
"elementId": "ySjONQgN",
"focus": 0.5543371205300343,
"gap": 9.228790283203125
},
"endBinding": {
"elementId": "Ms8Qbmxl",
"focus": -0.32540480491697205,
"gap": 9.86468505859375
},
"lastCommittedPoint": null,
"startArrowhead": null,
"endArrowhead": "arrow",
"points": [
[
0,
0
],
[
182.0670166015625,
2.028594970703125
]
]
},
{
"type": "arrow",
"version": 82,
"versionNonce": 34982596,
"isDeleted": false,
"id": "91jbTV-L3y2-cSdbHohNC",
"fillStyle": "hachure",
"strokeWidth": 2,
"strokeStyle": "solid",
"roughness": 0,
"opacity": 100,
"angle": 0,
"x": -145.23517990112305,
"y": -15.440345764160156,
"strokeColor": "#1971c2",
"backgroundColor": "transparent",
"width": 181.55984497070312,
"height": 4.057220458984375,
"seed": 1679510596,
"groupIds": [],
"frameId": null,
"roundness": {
"type": 2
},
"boundElements": [],
"updated": 1691265098796,
"link": null,
"locked": false,
"startBinding": {
"elementId": "umhz7cma",
"focus": -0.2623356925341876,
"gap": 15.3289794921875
},
"endBinding": {
"elementId": "fIgvyELe",
"focus": 0.12077898520577408,
"gap": 7.8575439453125
},
"lastCommittedPoint": null,
"startArrowhead": null,
"endArrowhead": "arrow",
"points": [
[
0,
0
],
[
181.55984497070312,
-4.057220458984375
]
]
},
{
"type": "image",
"version": 53,
"versionNonce": 757648380,
"isDeleted": false,
"id": "GP57pZUX",
"fillStyle": "hachure",
"strokeWidth": 1,
"strokeStyle": "solid",
"roughness": 1,
"opacity": 100,
"angle": 0,
"x": 40.868578576916164,
"y": -97.34738660876259,
"strokeColor": "#000000",
"backgroundColor": "transparent",
"width": 34.52716321970283,
"height": 16.74044277318925,
"seed": 31251,
"groupIds": [],
"frameId": null,
"roundness": null,
"boundElements": [
{
"id": "uMUYXu6UL8g9FFdjKx1-h",
"type": "arrow"
},
{
"id": "G2qwQAt_V_swf9_N1wAG7",
"type": "arrow"
}
],
"updated": 1691265090248,
"link": null,
"locked": false,
"status": "pending",
"fileId": "e86fb20a0fab29858cb73aa3d24f682184d37ba9",
"scale": [
1,
1
]
},
{
"type": "image",
"version": 42,
"versionNonce": 302765764,
"isDeleted": false,
"id": "Ms8Qbmxl",
"fillStyle": "hachure",
"strokeWidth": 1,
"strokeStyle": "solid",
"roughness": 1,
"opacity": 100,
"angle": 0,
"x": 48.73983534054693,
"y": 61.514706412338896,
"strokeColor": "#000000",
"backgroundColor": "transparent",
"width": 32.984845004941285,
"height": 16.492422502470642,
"seed": 26798,
"groupIds": [],
"frameId": null,
"roundness": null,
"boundElements": [
{
"id": "uMUYXu6UL8g9FFdjKx1-h",
"type": "arrow"
},
{
"id": "zzDvrTfTjVv1EtK9IqXXJ",
"type": "arrow"
}
],
"updated": 1691265094905,
"link": null,
"locked": false,
"status": "pending",
"fileId": "c3851aa1bf9d449ca18d9830f16903b8c86f3d60",
"scale": [
1,
1
]
},
{
"type": "image",
"version": 47,
"versionNonce": 722744188,
"isDeleted": false,
"id": "fIgvyELe",
"fillStyle": "hachure",
"strokeWidth": 1,
"strokeStyle": "solid",
"roughness": 1,
"opacity": 100,
"angle": 0,
"x": 43.903183451043475,
"y": -27.35696434004779,
"strokeColor": "#000000",
"backgroundColor": "transparent",
"width": 35.558051127698214,
"height": 16.73320053068151,
"seed": 30350,
"groupIds": [],
"frameId": null,
"roundness": null,
"boundElements": [
{
"id": "91jbTV-L3y2-cSdbHohNC",
"type": "arrow"
}
],
"updated": 1691265098796,
"link": null,
"locked": false,
"status": "pending",
"fileId": "bf96edc28fe96280f0d9ced0cf0f563a01670363",
"scale": [
1,
1
]
},
{
"type": "image",
"version": 45,
"versionNonce": 1507970812,
"isDeleted": false,
"id": "r7Hck7fb",
"fillStyle": "hachure",
"strokeWidth": 1,
"strokeStyle": "solid",
"roughness": 1,
"opacity": 100,
"angle": 0,
"x": -64.20200598421326,
"y": -111.86316444476913,
"strokeColor": "#000000",
"backgroundColor": "transparent",
"width": 19.493588689617926,
"height": 11.285761872936694,
"seed": 47767,
"groupIds": [],
"frameId": null,
"roundness": null,
"boundElements": [],
"updated": 1691265109627,
"link": null,
"locked": false,
"status": "pending",
"fileId": "5295f28687e2c09bfd95e1c4254036c62eb98ab4",
"scale": [
1,
1
]
},
{
"type": "image",
"version": 100,
"versionNonce": 2011149764,
"isDeleted": false,
"id": "2Tgb8o7i",
"fillStyle": "hachure",
"strokeWidth": 1,
"strokeStyle": "solid",
"roughness": 1,
"opacity": 100,
"angle": 0,
"x": -65.21641028108826,
"y": 51.43929527202775,
"strokeColor": "#000000",
"backgroundColor": "transparent",
"width": 19.493588689617926,
"height": 11.285761872936694,
"seed": 37828,
"groupIds": [],
"frameId": null,
"roundness": null,
"boundElements": [],
"updated": 1691265116425,
"link": null,
"locked": false,
"status": "pending",
"fileId": "2b91de35e072c31a4d61d350c6e8643e22fd6465",
"scale": [
1,
1
]
},
{
"type": "image",
"version": 1,
"versionNonce": 619983927,
"isDeleted": false,
"id": "jFblPZEx",
"fillStyle": "hachure",
"strokeWidth": 1,
"strokeStyle": "solid",
"roughness": 1,
"opacity": 100,
"angle": 0,
"x": -65.21637976351013,
"y": -36.29776527484725,
"strokeColor": "#000000",
"backgroundColor": "transparent",
"width": 19.493588689617926,
"height": 11.285761872936694,
"seed": 99167,
"groupIds": [],
"frameId": null,
"roundness": null,
"boundElements": [],
"updated": 1691265114507,
"link": null,
"locked": false,
"status": "pending",
"fileId": "a551e6bf83c3345517072534e93163034cc68325",
"scale": [
1,
1
]
}
],
"appState": {
"theme": "light",
"viewBackgroundColor": "#ffffff",
"currentItemStrokeColor": "#1971c2",
"currentItemBackgroundColor": "transparent",
"currentItemFillStyle": "hachure",
"currentItemStrokeWidth": 2,
"currentItemStrokeStyle": "solid",
"currentItemRoughness": 0,
"currentItemOpacity": 100,
"currentItemFontFamily": 1,
"currentItemFontSize": 20,
"currentItemTextAlign": "left",
"currentItemStartArrowhead": null,
"currentItemEndArrowhead": "arrow",
"scrollX": 367.4230766296387,
"scrollY": 203.9734115600586,
"zoom": {
"value": 2
},
"currentItemRoundness": "round",
"gridSize": null,
"gridColor": {
"Bold": "#C9C9C9FF",
"Regular": "#EDEDEDFF"
},
"currentStrokeOptions": null,
"previousGridSize": null,
"frameRendering": {
"enabled": true,
"clip": true,
"name": true,
"outline": true
},
"objectsSnapModeEnabled": false
},
"files": {}
}%%