The functor between vector spaces and their duals is contravariant

up:: Contravariant Functor

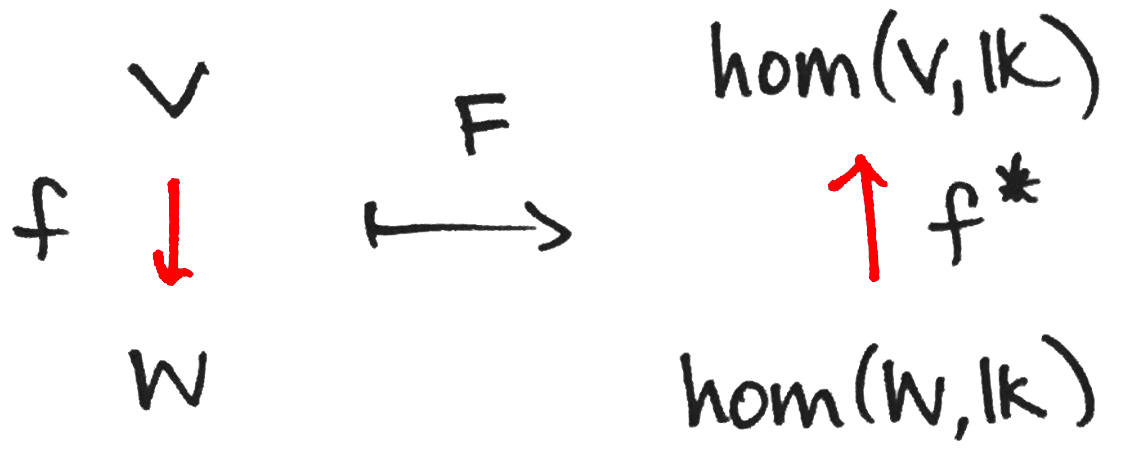
One can create a Functor between the Vect Category and their Vector Space Duals (i.e. their respective Hom-Sets to their underlying Field ).

That is, given Vector Spaces related by a morphism , we seek to know the form of . As it turns out,

not the other way around, which makes a Contravariant Functor. We denote : it is called ‘s Pullback.

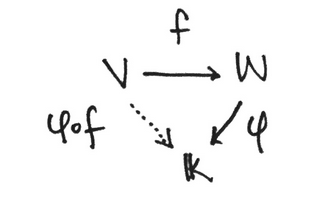
The way acts is as follows: For any Linear Operator , we have that

Finally, for any , we have that

Functorial properties

For any two morphisms

we have that, given some ,

Thus, we have that , and satisfies a functor’s properties.

---

References

• What is a Functor? Definitions and Examples, Part 2