Category

up:: 027 MOC Category Theory

A category is composed of:

1. A class of elements called objects, denoted
2. For each pair of objects , a class of elements called morphisms between and (called Hom-Set of morphisms from to ─ though it need not be a set)¹
3. For each pair of morphisms , a morphism , called their composite
4. For each object , an identity morphism

The rules that apply to a category are:

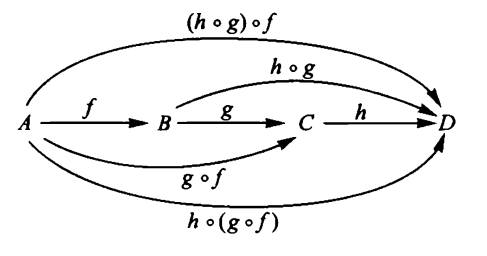
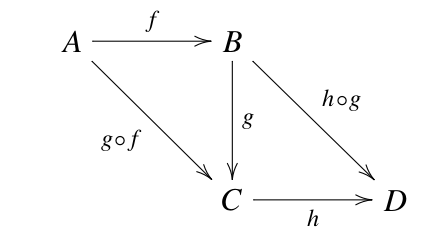
1. Composition of morphism is associative:
   
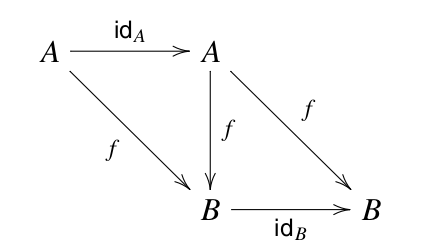
2. Identity morphism acts as two-sided composition identity:
   

Properties

• To every category there is an Opposite Category which is the same category but with all morphisms flipped

---

References

• category in nLab
• Category (mathematics) - Wikipedia
• ABRAMSKY, Samson; TZEVELEKOS, Nikos. Introduction to categories and categorical logic. In: New Structures for Physics, p. 3-94, 2011.

Footnotes

1. The class of all morphisms in is the disjoint union of all , for all . ↩