Desigualdade de Chebyshev

up:: 064 MOC Estatística em Economia

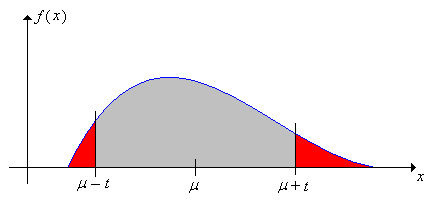
A desigualdade de Chebyshev explica a relação entre variância e o spread de uma variável aleatória com relação à sua média. É dela que vem a noção de que a variância é a “amplitude” de uma distribuição de probabilidade.

Equivalentemente, diz que o peso das caudas de uma distribuição de probabilidade possuem um upper-bound baseado na variância.

Seja uma variável aleatória, e sejam

Então, para todo ,

Demonstração

Note-se que, como , temos que

Portanto, o resultado segue trivialmente da Desigualdade de Markov:

Corolários

Tendo , temos trivialmente que, para qualquer ,

Ou seja, para a regra heurística usual de ” sigmas”, temos que a probabilidade do evento estar dentro de é igual a . Este upper-bound é bem relaxado quando comparado com o que certas distribuições conseguem, como a distribuição normal ().

---

References

• Variance
• 19. Weak Law of Large Numbers - YouTube