Transitive Group Action

up:: Group Action

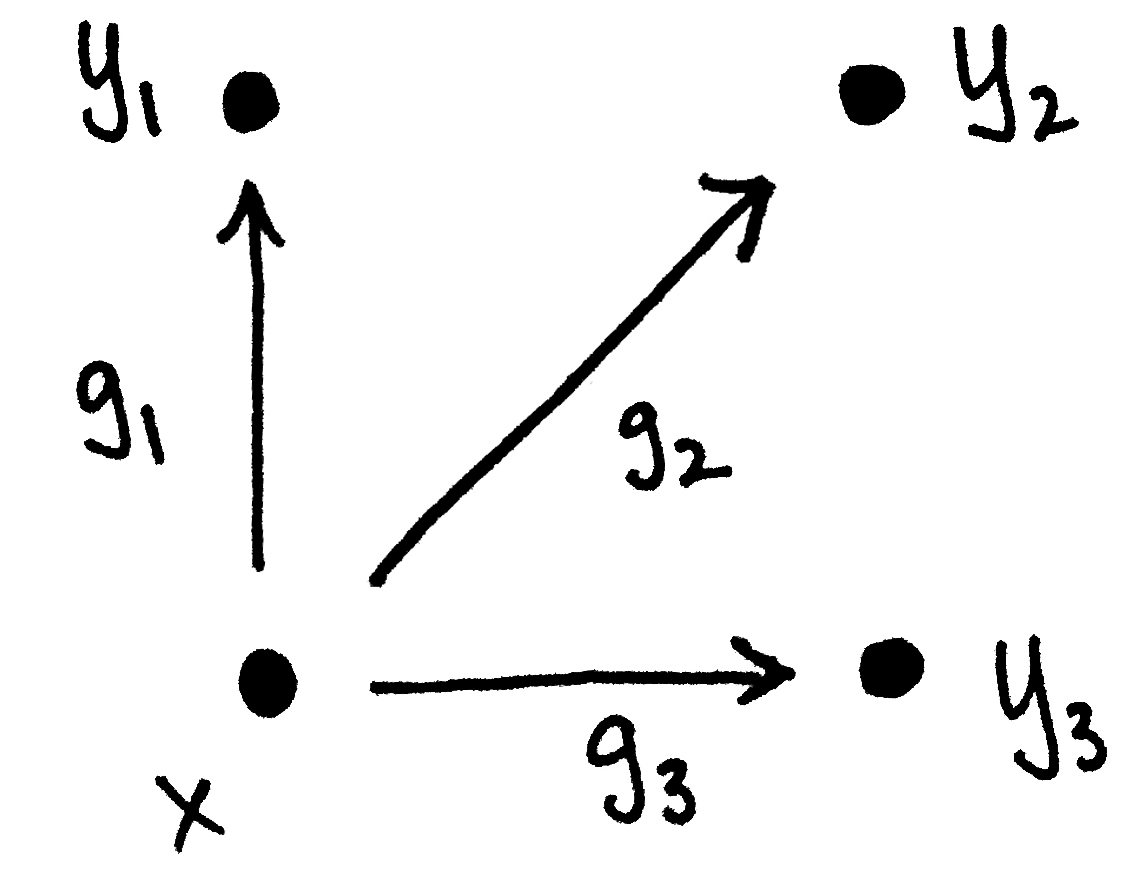
A Group Action is said to be transitive if, for any two points in the base space , there exists some element in the group which “connects” them.

That is, given a base space and a Group which acts upon (e.g. on the left),

Corollary

Transitive Group Actions are Surjective, since for all points , such that .

---

References

• Group action - Wikipedia