up:: index
Essa é uma apresentação que fiz para pessoas de Humanas como um primeiro contato ao Cálculo Diferencial e Integral, em fevereiro de 2024. Obviamente não possui todo o rigor de uma apresentação matemática, porém não é este seu propósito; serve como uma apresentação desta disciplina a pessoas que tendem a procurar a história/sociologia/filosofia/etc que permeiam as descobertas matemáticas, acanhando-se sempre de ver a Matemática de fato envolvida. Esta apresentação é, portanto, mais parecida com uma “terapia de choque” ─ porém num bom sentido (espero)!
O que é um limite?
.png)
Seja um polígono de lados, e um círculo. Conforme aumenta, se aproxima de um círculo .
Em notação matemática, escreveríamos
a ser lido como “conforme tende a infinito, se aproxima de “. Em outras palavras, conforme aumenta arbitrariamente, parece-se arbitrariamente próximo de . Obviamente, no exemplo acima, “parecer com ” não é precisamente “bem definido”, mas espero que a visualização faça com que o conceito seja claro.
Inclusive, perceba, conforme for lendo, que os verbos que são utilizados não são mera coincidência: “tender a”, “se aproximar de”, são verbos que indicam movimento ─ no fim das contas, essa é a essência do Cálculo.
Limites de funções
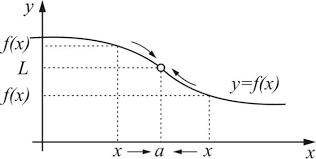
Note que, na imagem, conforme se aproxima de (eixo horizontal), se aproxima de (eixo vertical/altura). Escrevemos isso como
Caso , dizemos que é contínua no ponto . É similar à noção cotidiana de algo ser “contínuo”: um movimento contínuo sobre uma superfície é um movimento que consegue ocorrer desimpedido em seu processo, de seu começo a seu fim, por assim dizer. Inclusive, muitas pessoas aprendem que uma função é contínua quando consegue-se escrever ela “sem tirar a caneta do papel” enquanto se desenha ela.
Uma função descontínua
Destaque-se, porém, que nem sempre o limite de uma função é igual a seu valor no ponto! Ou seja, existem funções que não são contínuas, como, por exemplo,
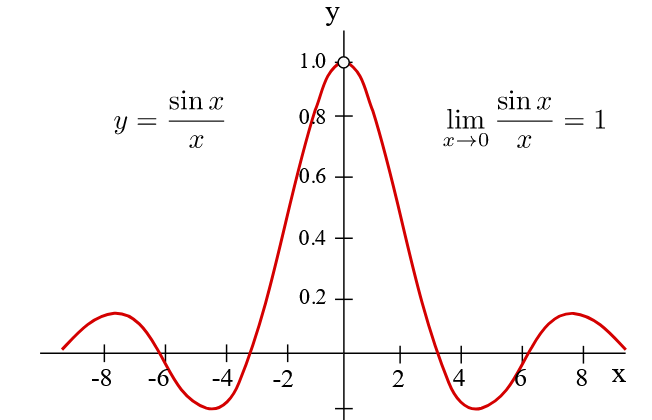
Note que não podemos calcular , pois não podemos dividir por ; porém, ela possui um limite conforme1 (é uma demonstração comum em Cálculo, através do chamado “teorema do sanduíche”/“squeeze theorem”).
O que é uma integral?
A definição usual do que é uma integral é “a área debaixo de uma curva”, a qual pode ser calculada através da soma de vários retângulos cujas larguras tendem a , como a área de um semi-círculo2:
Enfim, pode-se ver que podemos calcular a área debaixo de curvas através dessa soma de retângulos cada vez mais finos3 ─ ou seja, a integral é o limite dessa soma de retângulos (de largura e altura ). Denotamos esse limite como
O símbolo da integral é , que era um S originalmente mas foi “alongando-se” ao longo do tempo (não sei por quê). Note-se que denota-se a “fronteira” dentro da qual estamos buscando a área debaixo da curva: queremos a área de com , denotado por
Destaque-se que é para ser lido como se fosse, de fato, uma soma: estamos somando infinitos retângulos de altura e “largura” , com a ressalva de que o tamanho de é “infinitesimal”, tem “largura “. Não é rigoroso dizer isso, mas é a ideia do que está acontecendo: é como se fosse o limite da largura dos retângulos que vamos contraindo paulatinamente, de forma a obter uma medida mais e mais assertiva da área sob a curva. Embora os retângulos individuais tenham suas respectivas áreas indo a , em conjunto elas formam um “continuum” que compõe a área da curva, algo que é, por assim dizer, “maciço”, não-nulo.
O que é uma derivada?
O problema das velocidades médias
A velocidade média com que se percorre uma distância em um intervalo de tempo é definida como
Por si só, essa medida pode ser contraproducente quando mas , i.e. em funções não-lineares. Por exemplo:
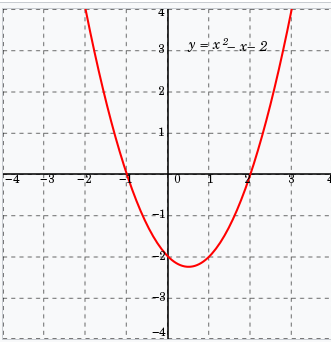
Pensando na “velocidade média” dessa função acima, entre e , teríamos que
O problema é visível pelo gráfico: vemos que a função muda de uma maneira que não é linear, e velocidades médias medem variações lineares ─ por isso é uma variação média! Buscamos, então, uma forma mais fidedigna de medir variações de funções, uma forma mais assertiva e “fina” o suficiente.
Definição de Derivada
Uma visualização gráfica explica muito bem o que é o conceito de derivada: ela é o limite de uma velocidade média. Quando falamos de uma “velocidade média”, estamos essencialmente medindo o coeficiente de uma reta, e retas sempre precisam de (ao menos) dois pontos para serem definidas; é por isso que a velocidade em um dado instante é um limite, é uma tendência à qual o movimento aproxima-se, conforme mede-se de maneira mais e mais “granular”.
Uma forma que gosto de pensar é a seguinte: para saber da posição de algum objeto4, preciso de ao menos uma “fotografia” sua, que indique sua posição e tempo com relação a algum ponto de referência fixo. Para saber sua velocidade, preciso de ao menos duas fotografias (com respectivos tempos), e a partir delas eu posso “extrapolar” o quão rápido ele deslocou-se entre uma e outra. É óbvio de pensar que, se eu tirar fotos em intervalos de dias, minha extrapolação será menos “fiel” ao movimento de fato do que se eu tirá-las, digamos, num intervalo de segundos. Aqui é importante também notar que, se eu tirar três fotos, eu posso extrapolar como sua velocidade variou: posso estimar uma velocidade média entre as fotos 1 e 2, e outra velocidade entre as fotos 2 e 3, e portanto uma aceleração (variação da velocidade) média entre ambos os pares de fotos; mutatis mutandis referente à discussão acima, tais extrapolações serão mais fidedignas conforme suas medições forem “mais granulares”. Essa é a intuição da derivada, que é um limite de uma variação média: o limite é justamente o mais “granular” que pode-se chegar nestas “medições” (obviamente ideais).
Derivadas fundamentais
Função constante
A derivada de uma função constante
é , pois
Isso corresponde a que a inclinação (ou “coeficiente angular”) de uma função constante é , ou seja, horizontal.
Função linear
A derivada de uma função linear
com , é
Ou seja, a derivada de uma função linear é o próprio coeficiente angular dela.
Função quadrática e além
A derivada de uma função quadrática
é
É simples (um pouco longo, via binômio de Newton) demonstrar que, para uma função , temos que
que é o que costuma-se chamar de “regra do tombo”, pois a derivada “tomba” o expoente e diminui-o por .
Antiderivadas
Dada uma função , temos que sua antiderivada é uma outra função que satisfaça
Ou seja, é a “operação” oposta da derivada.
Um exemplo usual é de que a posição é a antiderivada da velocidade, a velocidade é a antiderivada da aceleração, etc.
Note-se que tomar a antiderivada de é , pois
e é o “inverso” da regra do tombo.
Teorema Fundamental do Cálculo
O resultado basilar de Cálculo Diferencial e Integral é o Teorema Fundamental do Cálculo: fazer uma integral é tomar uma anti-derivada!
Ou seja, derivada e integral são operações inversas umas às outras!
Exemplo: Movimento Uniformemente Variado (MUV)
Um corpo está em movimento uniformemente variado quando sua aceleração é constante. Como a aceleração é a derivada da velocidade
eu posso integrar essa equação para obter a velocidade do corpo5
Posso fazer a mesma coisa de novo: a velocidade é a derivada da posição6
Integrando a equação novamente, e usando o resultado acima, obtemos
Ou seja, as equações básicas de cinemática que aprendemos no Ensino Médio requerem Cálculo para serem obtidas. Não caíram do céu! O não era ao acaso! E, de fato, este é o ponto: qualquer lei física que aprendemos na escola veio de alguma derivação matemática7.
O que mais?
2ª Lei de Newton
Equação de Euler-Lagrange (Mecânica Clássica)
Equação de Onda
Equação de Schrödinger (Mecânica Quântica)
Equação de Black-Scholes (Mercados financeiros)
…e por aí vai. Cálculo Diferencial e Integral é o bê-a-bá das Ciências Exatas como um todo; perguntar se cientistas utilizam Cálculo é tão esdrúxulo quanto perguntar se poetas usam palavras ou se biólogos usam a teoria de Darwin. É literalmente o capítulo 0 versículo 0, em particular, de todo o sucesso que a Física teve em explicar fenômenos tão drasticamente díspares quanto ondas gravitacionais e partículas elementares. Mas não tome minhas palavras com tanto peso; tome-as de um dos maiores matemáticos do século XX:
“O Cálculo foi a primeira realização da matemática moderna, e é difícil superestimar sua importância. Creio que ele define, mais do que qualquer outra coisa, a concepção de matemática moderna; e o sistema de análise matemática, que é seu desenvolvimento lógico, ainda constitui o maior avanço técnico em pensamento exato.”
(John von Neumann)
Todo começo é difícil, mas a prática e a perseverança são fundamentais. Não consegui encontrar de qual autor eu li uma vez, num prefácio, que dizia que aprender Matemática requer uma leitura com lápis e papel sempre a postos. Isto é justamente o que torna as Ciências Exatas tão “precisas”8: há conclusões que não são intuitivas, mas que são racionalmente deriváveis através de argumentos lógicos e bem delimitados; são conclusões, portanto, assertivas9. Enfim, tudo para dizer que é importante não depender exclusivamente do que a intuição nos diz; muitas vezes é preciso sentar, pegar caneta e papel, e fazer contas, invés de lançar conjecturas infalseáveis sobre o mundo (como muitos fazem por aí…).
Matemática se assemelha muito à arte em vários aspectos, e não são poucos os matemáticos que submetem-se a tanta burocracia acadêmica puramente por este sentimento de beleza e de sublime que ela evoca. Inclusive, talvez como a arte, existe uma satisfação criadora em estudar Matemática (ou qualquer área correlata): quando demonstro algum resultado, por mais que ele tenha sido demonstrado originalmente10 há séculos ou milênios ou décadas atrás, estabeleço um vínculo com o problema; ele, de certa forma, torna-se meu, torna-se uma besta recém-domada; aquilo que era algo originalmente “impenetrável” torna-se, de certa forma, “meu”, peculiarmente familiar e íntimo.
Há, neste fazer, algo de ímpeto criador, pois demonstrações matemáticas, por mais que possuam “regras” bem delimitadas (referentes à Lógica Proposicional, em particular), não são algo que apreende-se puramente “de fora para dentro”: Matemática é feita por outros seres humanos e, portanto, tanto parte de intuições que são intrinsecamente humanas quanto produz resultados que devem ser aferidos pela intuição humana11; decorre que minha verdadeira compreensão de algum problema matemático requerem um envolvimento de minha parte, requerem que eu esteja ali “de corpo e alma” e que apreenda o problema de forma intuitiva (para mim) e lógica (para mim e pelo rigor do resultado).
É algo desmoralizante quando nos introduzimos a alguém e ouvimos “nossa, eu odeio/odiava Física/Matemática na escola” ou “Física/Matemática é/era muito chato”. É compreensível, pois o que somos ensinados na escola não é, em absoluto, parecido com o que estuda-se na faculdade (ainda mais para Matemática!). Nos últimos anos houve um boom de vídeos no YouTube, que buscam elucidar a paixão que é possível sentir pela Matemática. No âmago de quem trabalha com Matemática há uma alma curiosa e vivaz, que busca padrões que a Natureza aponta-nos, mas não concede-nos12.
Posfácio (240720)
Quando possuo algo que fica “entalado na garganta”, eu me coloco a escrever para me acalmar; se os escritos que saem disso servem de ajuda aos outros, tanto melhor. Quando apresentei esse “seminário” a um grupo de militantes13, a seção de perguntas não me surpreendeu: um período transiente de pessoas que gostaram da apresentação e tiveram sua curiosidade atiçada (que foi muito bonito e me deixou feliz!), seguido pela arrogância costumeira do jovem militante marxista médio, que claramente sabe do que está falando, sempre. Escrevo agora, 5 meses depois da apresentação, pois estava relendo meu caderno de notas e isso me atiçou a escrever. Portanto, disclaimer: Há certas partes que posso lembrar incorretamente das falas ultra-pertinentes de meus interlocutores sagazes e veteranos14.
Alguns dos pontos de crítica trazidos são os seguintes.
1) A discussão sobre “experimentos” em Ciências
Houve uma fala sobre algo do tipo de que “experimentos são uma manifestação fetichista da visão da realidade”, quase como se fosse um “pulo lógico” extrapolar leis universais através de resultados tão particulares e “artificiais”, posto que são tão “sanitizados” e até distantes do que “realmente” acontece no mundo real.
Ora, se for assim, então joguemos a filosofia grega inteira fora. Não é como se eles só olhassem pro mundo platônico das ideias! Como pode que um cabra conseguiu medir o raio da Terra com duas varetinhas!? Como pode que um cara usou a água da banheira pra saber se uma coroa era de ouro ou prata!?
O tempo inteiro nós, cientistas ou leigos, temos uma hipótese implícita em nossos juízos sobre o mundo: de que ele é regido de maneira “ordenada”, chame-o de “leis da natureza”, chame-o de Razão, chame-o de Deus, o que seja; existem coisas que ocorrem de certa maneira previsível (tanto como outras infinitas coisas que não são tão previsíveis). Pela curiosidade que parece ser inata em nossa espécie, às vezes queremos sanar nossa curiosidade e descobrir se certo fenômeno é influenciado por algum outro fenômeno ou não; dessa forma, buscamos observar o fenômeno com e sem a presença do fenômeno , caso nos seja possível fazê-lo; caso não seja possível fazê-lo, utilizamos de deduções lógicas para tentar concluir alguma coisa. Nem tome isso como vindo de mim; tome de Marx:
“O físico observa processos naturais, em que eles aparecem mais nitidamente e menos obscurecidos por influências perturbadoras ou, quando possível, realiza experimentos em condições que asseguram o transcurso puro do processo.” (MARX, 2013, p. 78 [Prefácio da primeira edição]; grifo meu)
Pensar que as Ciências Exatas são mais suscetíveis ao pecado de serem enviesadas “só porque” dependem de experimentos isolados é adotar uma visão bem não-materialista: sem ter o pé no chão material, o sonho da razão produz monstros.
Adendo 250107
“Nas ciências da natureza, os cientistas contam, todavia, com um procedimento que contribui muito para o isolamento de categorias e relações de causa e efeito: a atividade experimental. Caso se pretenda apreender a importância epistemológica e mesmo a razão de ser da atividade experimental, deve-se salientar que o cientista produz um ambiente artificial com o propósito de ‘isolar’ uma parte da realidade, impedindo assim a ação de determinadas forças e reduzindo o papel do acaso. A criação do ambiente experimental é particularmente importante para que uma determinada lei, cuja manifestação é obstada” (i.e. impedida) “por outras determinações do mundo, exiba seu poder causal empiricamente. Constitui-se, assim, uma experiência diferenciada, que deve ser passível de reprodução para que o experimento tenha importância epistemológica” (MEDEIROS & BONENTE, p. 88; grifo meu)
…ao que adicionam logo numa nota de rodapé com o experimento usual de tampar uma vela acesa com um copo, para verificar que ela se apaga depois de um tempo. “Notem, por fim, que uma sequência regular entre dois eventos (evento A: cobre-se a vela acesa com um copo; evento B: a chama cessa após um decurso de tempo) é, portanto, criada pelo sujeito que conduz o experimento, mas não aquilo cuja existência o experimento permite revelar: o oxigênio” (ibid., destaque no original).
Ou seja, a ideia de um experimento é, em última instância, a determinação de como alguma lei específica afeta algum dado fenômeno — não de que o fenômeno estudado é afetado exclusivamente por esta lei! A experimentação nas ciências exatas sempre têm, implicitamente, a hipótese de totalidade concreta em que seus fenômenos de estudo jazem.
2) Ciência Tecnociência
Em Ciências Humanas, parece-me que falar “da Ciência” assume um claro valor de juízo duplo: quando incluem-se nessa “Ciência”, ela aparece como algo bom, variada e abrangente, interessante e até importante para a sociedade; quando excluem-se dela, ela torna-se ideológica, destrutiva, abreviam palavras e chamam-na diretamente de capitalista. Consideram que a Ciência é exclusivamente aquilo que legamos da aurora do Capital, financiada pelas (e para as) grandes navegações europeias.
Conforme o tempo passa, e especialmente lendo o livro “Discurso Filosófico da Acumulação Primitiva” (em particular a seção sobre Francis Bacon), admito que há um mérito nessa discussão; ela é, sim, pertinente.
Porém… eu sei muito bem quando alguém está fingindo saber de algo que eu sei melhor, e o discurso de quem é de Humanas e quer pagar que sabe de Exatas é muito pastelão. É algo que é incendiário sem propósito, é edgy só porque sim; mais me parece com começar uma briga sobre política em um churrasco em que todos estão conversando calmamente: essa discussão vai ser “útil” mesmo? There’s a time and place for everything…
O que cabe discernir é Ciência de Tecnociência: Tecnociência é algo muito recente, e é uma parte da Ciência como um todo. Aristóteles fazia tecnociência? Eratóstenes fazia tecnociência? Parece anacrônico. E, no entanto, me parece que faziam algo mais parecido com Ciência: observavam fenômenos que possuíam alguma “periodicidade” ou “padrão”, buscaram reproduzi-los de formas isoladas a fim de poder discernir o que lhes era pertinente do que lhes era contingente; em algum momento, e caso sua descrição dos problemas que abordavam fosse precisa e aderente o suficiente, chegariam a uma descrição dos fenômenos e de seus “porquês”, tirariam-lhes o véu mágico que concede-se a tudo aquilo que não sabemos de onde vem, e inseririam tal fenômeno numa totalidade de fenômenos conhecidos do Homem, podendo até mesmo possuir interrelações com alguns outros destes fenômenos previamente conhecidos.
Mas ora bolas, parece até que estou falando de Marx!
“Por isso, se eu começasse pela população [num estudo de economia política], esta seria uma representação caótica do todo e, por meio de uma determinação mais precisa, chegaria analiticamente a conceitos cada vez mais simples; do concreto representado [chegaria] a conceitos abstratos [Abstrakta] cada vez mais finos, até que tivesse chegado às determinações mais simples. Daí teria de dar início à viagem de retorno até que finalmente chegasse de novo à população [objeto de estudo], mas desta vez não como a representação caótica de um todo, mas como uma rica totalidade de muitas determinações e relações.” (MARX, 2015, p. 77; destaques em itálico meus)
3) “Cientistas trabalham a favor do Capital”
Dizer que as Ciências Exatas têm rabo preso com o Capital não é de todo mentira, credit where it’s due. Em particular nos Estados Unidos, por exemplo, os complexos militares são financiadores gigantes de cientistas. Contudo, chame-me de ingênuo ou o que seja, mas ninguém faz Ciência puramente para ganhar dinheiro: existem formas bem mais simples de ganhar bem mais dinheiro! Pelo amor de Deus, tem gente criando proficiência de quântica para business! Existe dinheiro pra caramba investido em artigos falando pura abobrinha quântica! Se restarem escrúpulos, trabalhar em análise de dados no mercado financeiro já dá um bom dinheiro, porque fazer contas básicas em planilhas de Excel e códigos simples em Python já são, para o indivíduo corporativo, de uma complexidade surpreendente.
Não venham dizer que o cara que estuda sobre teoria de nós também é lacaio do capital, ou que o cara que estuda gravitação quântica e teorias de gauge15 é um peão do capitalista que sabe o usufruto que terá dessa área de pesquisa – área esta, diga-se de passagem, na qual cientistas do mundo inteiro estão há décadas tentando fazer uma baita Aufhebung de duas teorias físicas extremamente sólidas e bem-comprovadas, que supostamente descrevem o mesmo mundo mas são tão, tão distantes uma da outra.
No meu primeiro dia da semana de calouros, no curso de Engenharia Física na EEL-USP, nosso veterano perguntou “quanto de vocês queriam fazer Física, mas fizeram engenharia pra agradar os pais?“. Uma boa parte dos mais de 40 bixos levantou a mão. Ora, Física não tinha rabo preso com o Capital? Que houve?
Quando transferi para a Física, claramente dava pra ver que o estudante médio de Física possui uma admiração enorme pelo mundo, de entendê-lo além da aparência caótica que ele apresenta a fim de penetrar “o garrido tumulto dos acontecimentos”16, de compreendê-lo profundamente a partir de primeiros princípios. E se tal brilho nos olhos perde-se com o tempo, ou esquece-se que ele foi uma motivação enorme outrora, devido às necessidades de pagar para viver e viver para pagar contas, então claro está que não é a totalidade das Ciências que são pau-mandado do Capital; o que pode-se afirmar é que podem ter sido cooptadas pelo Capital, pela promessa de dinheiro, segundo os ingênuos, e pela ameaça de morar na rua, segundo os realistas (afinal, se não pode contra eles, junte-se a eles).
Mas as Ciências não são totalmente cooptadas. Assim como o capitalismo de redes não é capaz de enfim apagar a chama revolucionária, a burocracia acadêmica e a cooptação capitalista não são capazes de suplantar a verdadeira motivação que propele as Ciências em geral: a paixão pelo conhecimento, a obsessão que temos de desvendar o mundo em que vivemos, e o fato impressionante de que não somos os únicos indivíduos dispostos a passar anos lendo tudo o que conseguimos sobre assuntos ultra específicos e escrevendo textos que provavelmente pouquíssimas pessoas lerão.
Tecnociência é Ciência, mas Ciência é mais do que tecnociência, que é um braço extremamente bem cooptado da Física, Química e Engenharia17 pelo Capital.
Concluindo…
“Na medida em que eu parto do reconhecimento do teu direito de dizer a palavra, quando eu falo porque te ouvi, eu faço mais do que falar a ti, eu falo contigo. Mas, falar a ti só se converte no falar contigo, se eu te escuto.” (FREIRE, 2012; grifo meu)
O que mais me frustrou na minha breve passagem de dois anos pela militância jovem é a desonestidade intelectual que se tem quanto a ideias que lhes sejam alheias. E para jogar-lhes denúncias – que vestem-se de políticas mas, em verdade, têm cunho moral –, abundam palavras: “esquerdista”, “autonomista”, outros -istas talvez (até “anarquista”, como se fosse algo ruim).
Minha apresentação buscava mostrar a beleza das ideias do Cálculo Diferencial e Integral, e de como podemos descrever o mundo de forma bem satisfatória com elas18. Se aqui cabem críticas quanto ao seu surgimento histórico, eu bem poderia criticar que Marx conseguiu escrever tanta coisa porque Engels usufruiu muito bem do mais-valor que pôde extrair enquanto legatário das indústrias de seu pai; eu posso criticar sua influência hegeliana que vem de láaaaa desde os pensadores iluministas, os quais estavam bem em contradição com as ideias que eles próprios apresentavam19.
Meu propósito com minha apresentação foi de fazer aquilo que eu, desde minha participação na Coordenação Regional do Ecoar, busquei deixar explícito: mostrar algo que está fora da “visão” dos demais, buscar mostrar que o mundo é bem maior do que somente Marx, Lênin e Gramsci; furar bolhas a fim de prevenir vieses de confirmação que são tão fatais de ocorrerem em espaços tão homogêneos. O mundo não é somente o mundo dos homens, por mais que as cidades nos acostumem a ver somente aquilo que veio de seu punho (de ferro). Há beleza na Natureza não-humana, potência indomável em essência porém impressionantemente inteligível. Admirá-la e ver suas semelhanças com nossas vidas e estruturas sociais não é ser “fatalista”, ao menos não necessariamente. Acreditar que escapamos das leis da Natureza é acreditar que não somos por elas sujeitos, e isso não é uma visão muito materialista de se ter. Contudo, claro, ao mesmo tempo em que somos sujeitos a suas leis (gravidade, genética, etc), o que diferencia o homem do resto do mundo vivo é a capacidade que temos de sobrepujar nossos ímpetos intrínsecos. Afinal, não é “natural” que eu tenha gasto tanto tempo escrevendo uma crítica de comentários de pessoas que sequer vão me ler! (Digo “natural” no sentido de que a espécie da qual pertenço, Homo sapiens sapiens, não surgiu evolucionariamente de forma a ser imediatamente apta para tal ato específico, equivalente moral de “reclamar no Twitter/X”.)
Eu sei que todo esse debate frívolo que aconteceu na seção de perguntas após minha apresentação foram meramente pessoas que queriam pagar de espertas em algo que não sabem quase nada, e que precisavam se agarrar ao mínimo possível que tinham ao alcance para ter algo para falar, algo para impor-se e apoderar-se da conversa, “conquistar corações e mentes”, conscientizar. E ali foi a última gota para mim, porque eu cansei de ficar em espaços que querem falar para mim, que querem impor crenças em mim; eu quero espaços que falem comigo, nos quais eu seja sujeito e não mero objeto ou meio para um fim que me é alheio. Se nem mesmo o tópico no qual eu sou uma “autoridade”, ao menos no tocante aos demais que estavam presentes, então naquilo que eu não sou tão conhecedor, agirão para comigo como se eu fosse um mero recipiente de fatos e crenças e sopas de letrinhas – e sem receber um tostão por tal suplício!? Francamente, isso é chato pra caralho.
PS: Para quem tenha caído de paraquedas em toda essa diatribe, saiba que eu (ao menos ao momento da escrita), apesar dos pesares, considero-me marxista, sim! Se assim não fosse, eu não estaria tão dedicado a escrever minhas anotações sobre O Capital em formato Zettelkasten (vide 011 MOC Capital)! O problema não é Marx… são seus fãs. E o academicismo. Principalmente o academicismo. E tantos ismos. Ismos ismos, miaísmos.
Referências da apresentação
- 3Blue1Brown: Calculus Playlist é o santo Graal que muitos de nós (me incluo nisso) queríamos ter tido em nossos primeiros contatos com Cálculo. 3Blue1Brown foi um pioneiro fundamental no nicho de “animações matemáticas” do YouTube, e acredito que o ensino de Matemática como um todo está sob uma revolução há anos devido à sua influência e inspiração.
- STEWART, James. Cálculo, Volume I.
- GUIDORIZZI, Hamilton L. Um curso de cálculo. (Para os mais matematicamente inclinados/corajosos/curiosos; um paraíso para neurodivergentes excessivamente lógicos que odeiam fazer suposições sobre o por quê das coisas serem do jeito que são.)
Referências do posfácio
- MARX, Karl. O capital-Livro 1: Crítica da economia política. Livro 1: O processo de produção do capital. Boitempo Editorial, 2013.
- MARX, Karl. Grundrisse: manuscritos econômicos de 1857-1858: esboços da crítica da economia política. Boitempo Editorial, 2015. Disponível em: https://files.cercomp.ufg.br/weby/up/208/o/Karl_Marx_-_Grundrisse_(boitempo)_completo.pdf.
- OLIVEIRA, Pedro Rocha de. Discurso filosófico da acumulação primitiva: estudo sobre as origens do pensamento moderno. Editora Elefante, 2024.
- FREIRE, Paulo. Princípios do Trabalho Popular. In: Trabalho de Base (Seleção de roteiros organizados pelo Cepis), Ranolfo Peluso (org.), Expressão Popular, 2012. Disponível em: https://www.novacultura.info/post/2022/08/19/paulo-freire-principios-do-trabalho-popular
- MEDEIROS, João Leonardo; BONENTE, Bianca Imbiriba. Marx e a crítica da economia política: considerações metodológicas. In: MEDEIROS, João Leonardo; BARRETO, Eduardo Sá (Org.). Para que leiam O capital: interpretações sobre o Livro I. Usina Editorial, 2021.
Footnotes
-
Leia-se: “conforme tende a “. ↩
-
A quem interesse: a animação foi feita com o pacote Manim, do Python, em particular o Manim Community. Para os códigos que utilizei, conferir GitHub - nicholasvoltani/Manimations. ↩
-
Ao observador atento, pode-se perguntar “mas que ponto dentro do retângulo eu devo usar para medir a altura do respectivo retângulo?“. Note que na animação, por exemplo, pega-se as alturas dos pontos à esquerda dos retângulos. No fim das contas, não importa, pois estaremos tomando o limite em que “haverá somente uma altura” por retângulo. Inclusive, é por isso que é importante que a função a ser integrada seja contínua, pois é isso que assegura que pontos próximos tenham alturas próximas. Porém… ↩
-
Em algum sistema de coordenadas, digamos, por exemplo, da esquerda para a direita, em metros. ↩
-
Assumindo que o movimento começa em , por simplicidade, e definindo e ; o símbolo denota a “definição” de alguma variável (no caso, e ). Supor faria surgir vários termos da forma , e tornaria o exemplo mais opaco ao leitor mais leigo. ↩
-
\begin{rant} Uso a variável para denotar posição somente para remeter às fórmulas que aprendemos na escola, pois acho péssimo utilizar para medir posição (em metros pelo SI), sendo que medimos tempo pela unidade de segundos . Em nível universitário, geralmente usamos para denotar posições. \end{rant} ↩
-
Dificilmente estudamos na escola alguma equação que foi formulada fenomenologicamente (ou seja, sem ser a partir de primeiros princípios) ─ se estudamos, geralmente é por fins históricos e a fim de demonstrar a generalidade de alguma outra lei que a substitua (por exemplo, lei de Wien versus lei de Planck). ↩
-
Até mesmo a noção de probabilidade é precisa neste sentido: é uma teoria que nasce da própria lógica matemática e não lhe é algo contingente. Ironicamente, por mais que probabilidades meçam incertezas, sua teoria é extremamente bem-conhecida e estudada ativamente, e empregada em situações em que existem incertezas em medições ─ ou seja, em quase todo lugar (mileage may vary)! ↩
-
Quando encontra-se um contra-exemplo de alguma conclusão lógica, revisa-se as hipóteses empregadas em sua formulação, e corrige-se de acordo. É como o famoso problema de “todos os cisnes são brancos”. ↩
-
Há muitos resultados que são redescobertos em vários momentos da História por pessoas diferentes, assim como resultados que são descobertos mas não publicamente, mas escute-me… ↩
-
Similarmente, Toda obra de arte é criada para outras pessoas. ↩
-
Similarmente, A arte busca representar o mundo objetivo através de categorias humanas. ↩
-
Dissidentes do Ecoar - Juventude [Ecos]socialista, cf Sobre minha saída do Ecoar. E agora sou dissidente dos dissidentes, pode me chamar de “autonomista” ou “irracional”. Quem diria que certos camaradas que leem Jodi Dean podem ser tão filhos da puta! ↩
-
Sobre minha relação com a militância jovem: I know it’s part of the process, but Jesus Christ it hurts. ↩
-
Coitados dos pesquisadores de gravitação quântica, fazendo das tripas coração. ↩
-
HEGEL, Georg Wilhelm Friedrich. A razão na história. Ed. Leya, 2013, p. 34. Infelizmente o Jorge Grespan se aposentou, então suas incríveis aulas de Teoria da História ficarão nas lembranças de quem pôde vê-las.
241219: As aulas de Teoria da História do Grespan estão disponíveis no YouTube!!! Teoria da História I e Teoria da História II. POGGERS ↩ -
Dá pra se argumentar que Engenharia surgiu puramente devido ao desenvolvimento do Capital, mas enfim, não tenho opinião formada disso. ↩
-
Ok, Cálculo é uma forma satisfatória pela qual descrevemos o concreto no pensamento, caso queira ser tão pedante. ↩
-
Para os marxistas que amam Thomas More e sua Utopia, saibam que ele tinha um pelourinho em sua propriedade – e que a Utopia que ele descreve parece ser um inferno na Terra, em verdade! Novamente, leiam “Discurso Filosófico da Acumulação Primitiva”. ↩