Cartesian products in Set are categorical products

up:: Product (Category)

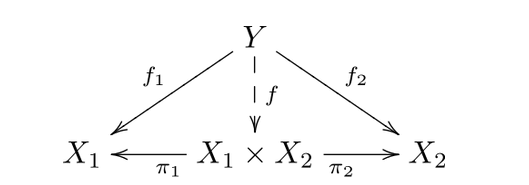
Given two sets , denote their cartesian product as , and let

be the respective projection maps.

Let be another set.

Every function to the cartesian product is completely determined by the projection maps

Let be any map.

Then it is uniquely determined by its values under composition with the projection maps, since

Functions to coordinate sets uniquely induce factor map to cartesian product

Conversely, let functions from to each “coordinate” set . Then there is a unique map such that

In fact, it is of the form

which is uniquely determined by and which satisfies the condition above.

Conclusion

Note that to every function

there is a unique function

where are uniquely determined by .

Thus, there is an isomorphism between the Hom-Sets and .

---

References

• MAC LANE, Saunders, Categories for the Working Mathematician, New York, NY: Springer New York, 1978.