up:: 041 MOC Graph Theory
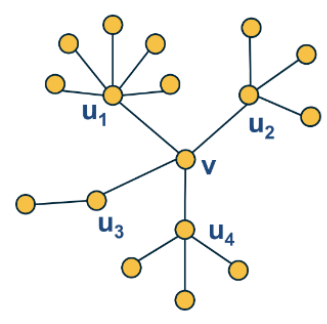
Example from 0_CS7280_NetworkScience, for ‘s average nearest neighbors degree, which is : note it takes into account paths from to itself as well!!!
Given a node from a graph with Adjacency Matrix , its average nearest neighbor degree is
That is, it is the weighted average degree from ‘s neighbors (weighted by ‘s row of the adjacency matrix). Do not forget that these degrees also take into account! In fact, A simple graph’s node is a (local) star graph center iff its average nearest neighbors degree equals 1!
in terms of powers of the adjacency matrix
One can also see this measure as referring to the second power of the adjacency matrix, i.e. to -paths coming out of :
References
- BOCCALETTI, S. et al. Complex networks: Structure and dynamics. Physics reports, v. 424, n. 4–5, p. 175–308, 2006.