The interior is the complement of the closure of the complement

up:: Interior (Topology)

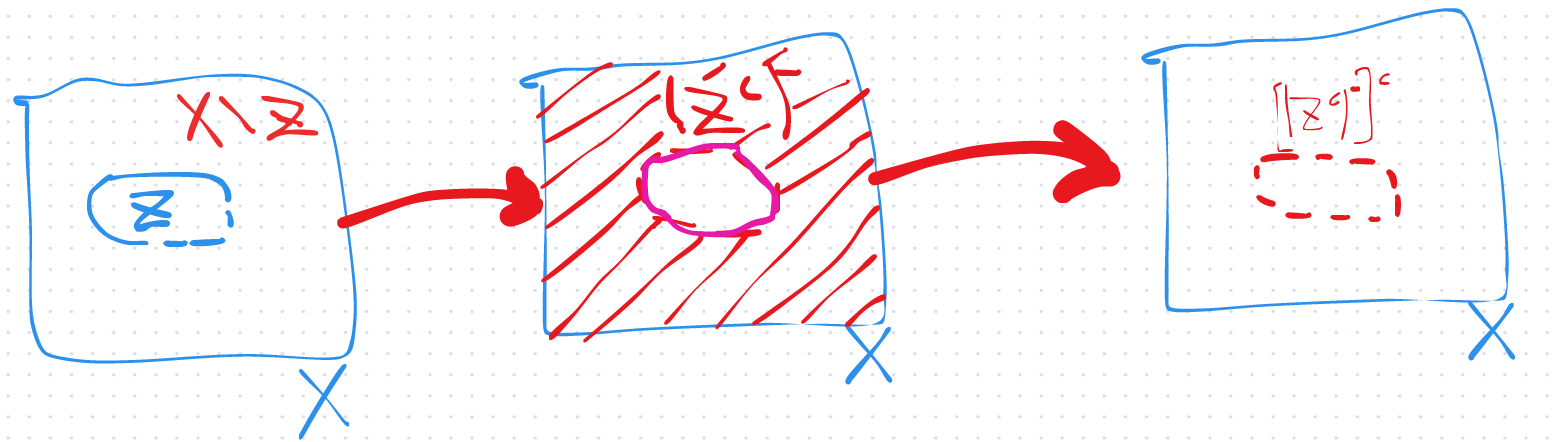
Let be a Topological Space, and a subset.

Then, since All sets contain their interior, .

Since Set Complements flip subset ordering, we have that . Since is open, is closed, and equal to its own Closure. Thus,

By flipping again with complements, we arrive at

which shows an open set¹, which contains ‘s interior. However, since is the largest open set contained in , then we have that

---

References

• Notas para um Curso de Física-Matemática, João Carlos Alves Barata. Cap. 27

Footnotes

1. Since the complement of an open set/interior is a closed set. ↩