The image of the intersection is contained in the intersection of the images

up:: Image of Function

Let be a function and subsets .

Then let a point in ‘s Image. Then

By the definition of the image of a function, we have that

Thus, . Note that the reciprocal need not necessarily hold, due to the implication holding only one way, generally: there can be more than one point mapping to , coming from and , and not necessarily from .

Counterexample of the equality

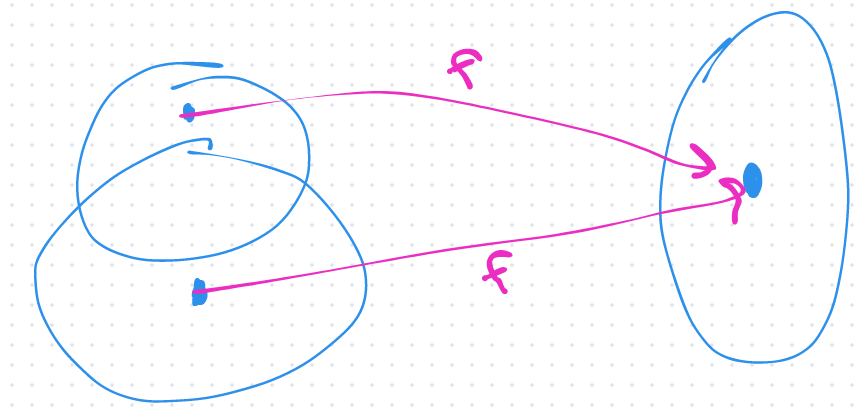
Let two non-overlapping sets map to the same point under . Then , and yet .

Thus, cases in which distinct points can map to the same point break the equality for images of intersections. That is why The injective image of intersections is the intersection of images.

---

References

• Sutherland, Wilson A. Introduction to metric and topological spaces. Oxford University Press, 2009.