The closure is the complement of the interior of the complement

up:: Closure (Topology)

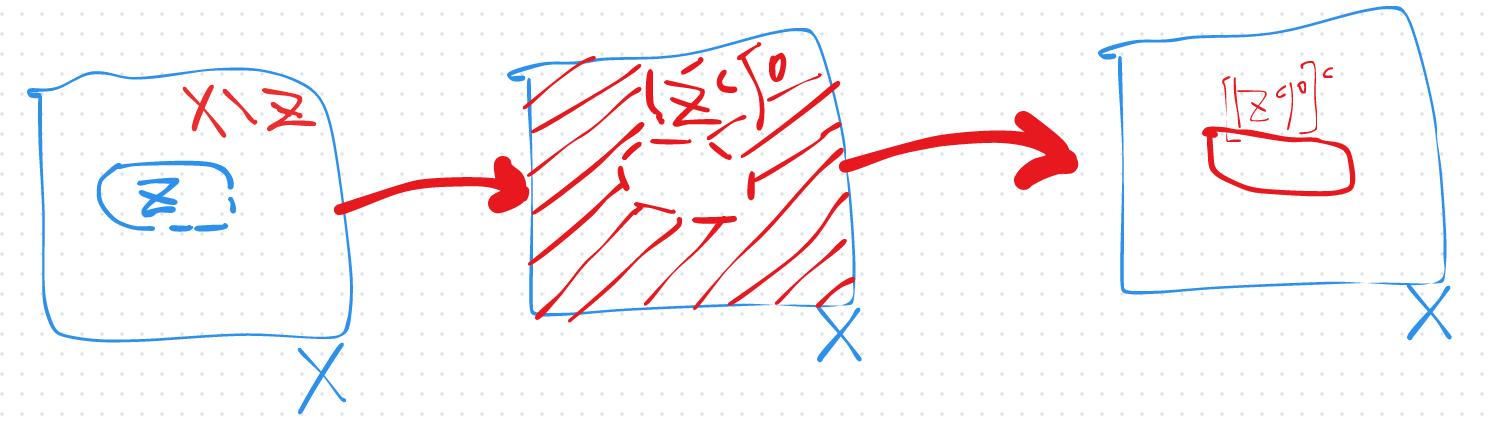
Let be a Topological Space, and a subset.

Then, since All sets are contained inside their closure, .

Since Set Complements flip subset ordering, we have that . Since is closed, is open, and equal to its own Interior. Thus,

By flipping again with complements, we arrive at

which shows a closed set¹, which is contained inside ‘s closure. However, since is the smallest closed set containing , then we have that

---

References

• Notas para um Curso de Física-Matemática, João Carlos Alves Barata. Cap. 27

Footnotes

1. Since the complement of an open set/interior is a closed set. ↩