Regressão Linear Múltipla

up:: 064 MOC Estatística em Economia

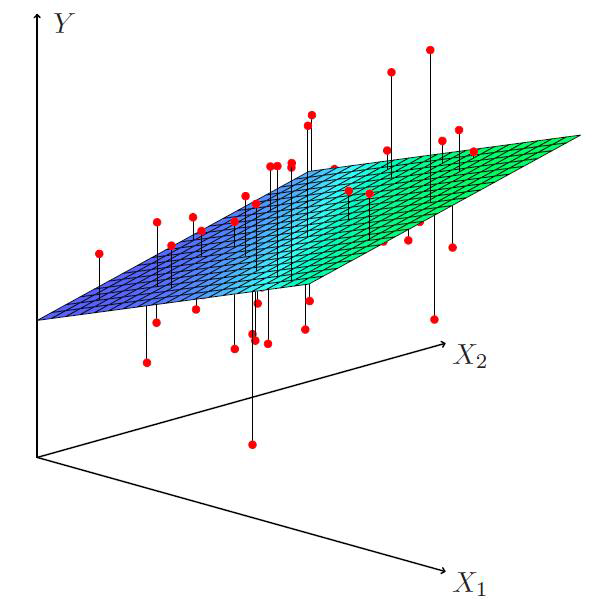
Fonte: Multiple Linear Regression-An intuitive approach | by Niketh Narasimhan | Analytics Vidhya | Medium

Um modelo de regressão linear múltipla segue a forma

onde

• (dependem da quantidade de observações)
• (depende da quantidade de características , mais viés )
• é a matriz de desenho (design matrix), que possui as observações das variáveis independentes

Para fazer uma regressão linear múltipla, seguem-se as hipóteses de Gauss-Markov:

1. 1. Portanto, ¹
2. 1. Portanto, ²

Solução de Mínimos Quadrados

Ao obter o mínimo do erro quadrático

obtém-se que a melhor estimativa para é³

Disso, obtém-se que a previsão de é

onde é uma matriz de projeção ortogonal⁴ ao plano determinado por .

Propriedades de

O valor esperado de é (vide propriedade 1 acima)

Portanto, é um Estimador Não-Enviesado.

A variância de é (vide propriedade acima)

Este estimador é o Melhor Estimador Linear Não-Enviesado de (ou seja, de menor variância dentre estimadores lineares) devido ao Teorema de Gauss-Markov.

---

References

• GUJARATI, Damodar N. Basic econometrics. 5ª edição.
• 09. Modelos de Regressão Linear Múltipla - Parte 1 - YouTube
• 6. Regression Analysis - YouTube
• A brief summary on Machine Learning (Nicholas Funari Voltani)

Footnotes

1. I.e. o preditor linear é igual ao valor esperado da variável que ele busca estimar, . ↩

2. Pois assume-se que a matriz de design é determinística (!!!) ↩

3. Estamos falando de estimadores, pois estamos fazendo mínimos quadrados, ou seja, estamos trabalhando com uma quantidade finita de dados, não com a distribuição estatística “verdadeira” de e . Pressupondo que “realmente”, então nossa melhor estimativa dessa relação, com nossos dados, será através de . ↩

4. Em inglês, alguns chamam ela de hat matrix, pois ela converte em (“Y-hat”). Cf. problem set do MIT. ↩