Subnetting (IP Networks)

What is subnetting?

A subnet mask yields which bits in a network IP are already occupied (called the routing prefix) and which are available (which are the host identifiers).

For instance, consider the mask 255.255.255.0. (in IPv4, i.e. 8 bits per “number” separated by dots) (Prints below are from the CyberMentor’s worksheet for subnetting.)

The number in each subnet mask is the sum of the powers of the active/occupied bits: when all (eight) bits are active, the sum evaluates to 255

The backslash notation indicates how many bits in total are active/occupied (in the case above, /24 means that 24 bits are active).

The number of total hosts available in a subnet is equal to to the power of the inactive bits (since each one can either be on/off), although usually the number is actually this total minus 2 (to account for the netmask address as well as the broadcast address).

Example

• The mask is 255.255.255.0: thus, only the last part is mutable, while the others are constant (i.e. all hosts will be of the form 192.168.57.x).
• The netmask address defaults to 192.168.57.0, the first available host
• The broadcast address defaults to 192.168.57.255, the last available host
• The number of free available hosts is, thus,

Rule for calculating subnet masks from unoccupied bits

Notice that

is the sum for occupied bits (i.e. unoccupied bits).

For unoccupied bit, the sum goes to . For unoccupied bits, the sum goes to etc.

Thus, for unoccupied bits, we have the formula for the corresponding subnet mask’s number

Notice that it generalizes even for the case of all () available bits, for which the respective submask number goes to (!).

Exercise

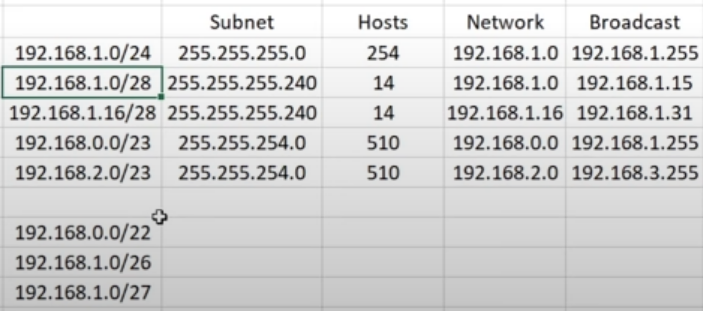
Network IP	Subnet	Available Hosts	Network	Broadcast
192.168.0.0/22	255.255..0		192.168.0.0	192.168.3.255
192.168.1.0/26	255.255.255.()		192.168.1.0	192.168.1.63
192.168.1.0/27	255.255.255.()		192.168.1.0	192.168.1.31