Open Sets in Metric Spaces

up:: Open Balls (Metric Spaces)

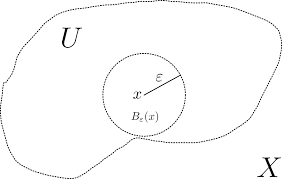
Given a Metric Space and some set , then is said to be open if, for all points , there exist some open ball with radius dependent on .

The set of all open sets in a metric space (as defined above) is called the Metric Topology, or metric-induced topology.

Generalization to Topological Spaces

Instead of thinking about open sets as being dependent on the metric structure of a space (i.e. containing some open ball around its points), a Topology is already the set which contains all open sets from the get-go.

---

References

• Notas para um Curso de Física-Matemática, João Carlos Alves Barata. Cap. 24