Lattice

up:: Universal Algebra

A triple is said to be a lattice if its functions satisfy the properties

• Idempotency:
• Commutativity:
• Associativity:
• Absorption Laws:

Examples

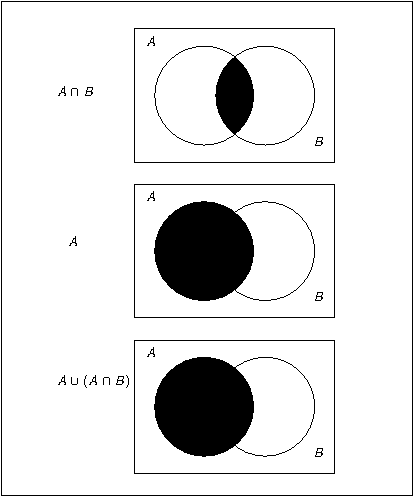
Given a set , its powerser , alongside the intersection and union operators, can be thought of as a lattice. In it, the absorption rules are clear:

Properties

For any lattice , it is true that

:
:

From this, it follows that Every lattice induces a partial ordering.

A lattice with global upper and lower bounds is said to be a Limited Lattice, whose maximum and minimum we denote as and , respectively.

When a lattice’s operators distribute, such as

it is called a Distributive Lattice.

---

References

• Notas para um Curso de Física-Matemática, João Carlos Alves Barata. Cap. 02
• discrete mathematics - absorption laws don’t understand it with Venn diagrams - Mathematics Stack Exchange