up:: Group Homomorphism
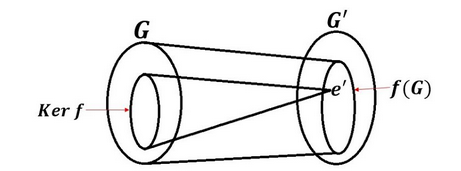
Given a mapping between groups , its kernel is defined as its “null space”, i.e. all elements which are mapped to the identity
Equivalently, it is the inverse image of the identity
up:: Group Homomorphism

Given a mapping between groups , its kernel is defined as its “null space”, i.e. all elements which are mapped to the identity
Equivalently, it is the inverse image of the identity