Hausdorff Space

up:: Topological Space

”For many mathematicians, the Hausdorff property is like having power in your apartment. Of course, you can build a space without it, but you kind of assume that it will be there. Doing topology without the Hausdorff property feels like stumbling around in the dark.” (Evelyn Lamb)

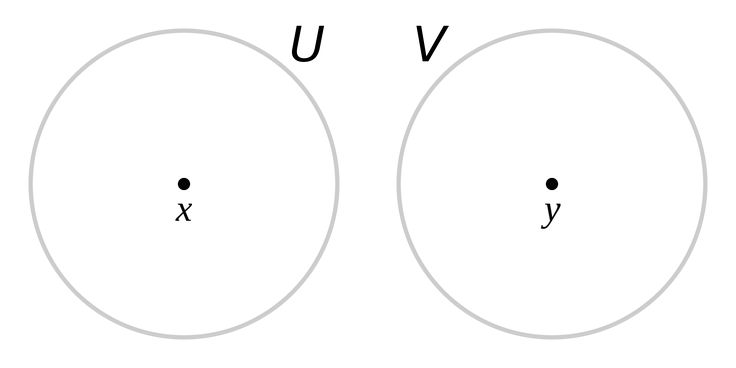
A topological space $(X,\tau )$ is called a Hausdorff space if, for any points $x,y\in X$, there exist open sets $U_x,U_y\in \tau$ such that $x\in U_x\perp U_y\ni y$¹.

Corolaries

An easy result is that All metric spaces are Hausdorff spaces.

Examples of non-Hausdorff spaces

• The line with two origins is a non-trivial example of a non-Hausdorff space: both origins aren’t separable by open sets, since they will always have some intersection elsewhere

---

References

• A Few of My Favorite Spaces: The Line with 2 Origins - Scientific American Blog Network
• Notas para um Curso de Física-Matemática, João Carlos Alves Barata. Cap. 30: Continuidade e Convergência em Espaços
  Topológicos

Footnotes

1. I define $U_x\perp U_y\equiv U_x\cap U_y=\varnothing$. ↩