Nicholas Funari Voltani

Galilean Space-time Structure

1 min read

up:: Euclidean Affine Space

A Galilean Space-time structure consists of:

  1. Event space: An Affine Space over a four-dimensional vector space over
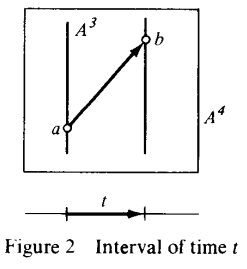
  2. Time map: A linear mapping which measures time intervals between parallel displacements
    1. Given events for which , then and are said to be Simultaneous Events (Galilean)
  3. Distance between simultaneous events: A distance between simultaneous events can be defined as . I.e. it uses the Vector Space Norm over which is induced by the Euclidean Structure’s Inner Product

An affine space with this structure is said to be a Galilean Space. Transformations which preserve this structure are called Galilean Transformations. Transformations which preserve the galilean structure are Galilean Isomorphisms.

References

  • ARNOL’D, Vladimir Igorevich. Mathematical methods of classical mechanics. Springer Science & Business Media, 2013.

Graph View

Backlinks