ANPEC Estatística 08 2023

up:: 064a MOC ANPEC Estatística

Questão sobre Teste de Hipótese.

Cálculos preliminares

As variáveis dadas são:

• $n=25$ número de amostras
• $\bar{X}=110$ é a média amostral
• $S^2=400$ é a variância amostral
  • Portanto, $\frac{\sqrt{S^2}}{\sqrt{n}}=4$ é o desvio padrão esperado
• $\mu =100$ é o valor esperado da hipótese nula
• $\alpha =0.10$ é o Nível de Significância, i.e. probabilidade de erro de tipo I
• É dado no enunciado que $P(-1.71<Z<1.71)=\alpha$, com $Z\sim N\left(\mu ,\frac{S^2}{n}\right)$

Item 0: Verdadeiro

Por definição, a probabilidade de tipo de erro I é chamada de nível de significância, $\alpha$.

Item 1: Falso

Temos que a região crítica é

$$RC=(-\infty ,-1.71]\cup [1.71,\infty )$$

no espaço-$Z$. Convertendo para o espaço de $\bar{X}$, temos

$$\begin{array}{rl}RC& =(-\infty ,100-1.71\cdot 4]\cup [100+1.71\cdot 4,\infty )\\ & =(-\infty ,93.16]\cup [106.84,\infty )\end{array}$$

Como temos que $\bar{X}=110\in RC$ pertence à região crítica, temos de rejeitar a hipótese nula.

Item 2: Falso

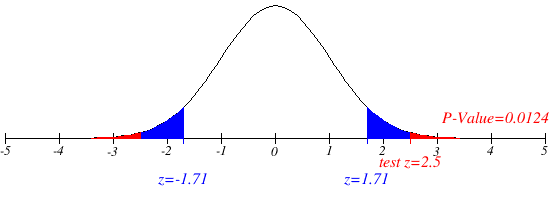
Fonte: Hypothesis Test Graph Generator

O p-valor deste problema consiste na probabilidade de eventos mais extremos do que o obtido ocorrerem. Porém, como rejeitamos a hipótese, temos que $\bar{X}\in RC$ está na região crítica; eventos mais extremos do que o $\bar{X}$ observado também estarão em RC, porém com probabilidade menor¹.

O que ocorre é o mostrado no gráfico acima. Para calcular o p-valor de fato, buscamos a chance de eventos deste tipo ou mais extremos do que $\bar{X}=110$ ocorrerem.

Portanto, buscamos

$$\begin{array}{rl}P(\bar{X}>110)& =P\left(Z>\frac{110-100}{4}\right)\\ & =P(Z>2.5)\\ & =1-P(Z\le 2.5)\end{array}$$

Como temos uma distribuição simétrica, multiplicamos esta probabilidade por $2$.

Item 3: Falso

O intervalo de confiança é

$$\mu \pm \sqrt{\frac{S^2}{n}}\cdot 1.71=100\pm 1.71\cdot 4$$

Tem de ser $\mu$, pois estamos falando do intervalo de confiança da distribuição da hipótese nula, a qual está centrada em $\mu$ e possui variância² $\frac{S^2}{n}$.

Item 4: Verdadeiro

O nível de significância $\alpha$ é cortado ao meio, portanto o intervalo de confiança encolhe-se em torno de $\mu =100$. Porém, consideram-se agora somente valores maiores do que $\mu =100$, i.e. $RC=[z,\infty )$, para o valor $z$ que satisfaça

$$P(Z\ge z\mid H_0)=0.05$$

Através da tabela z, obtém-se que $z\approx 1.645$, i.e. $RC=[106.58,\infty )$, ou seja, ainda rejeita-se a hipótese nula ($110\in RC$). Intuitivamente, como o p-valor anterior já era bem menor do que o nível de significância de 10%, essa mudança não foi suficiente para que o valor observado de $\bar{X}$ caísse dentro do intervalo de confiança (ou, em outras palavras, não foi suficiente para que ele caísse fora da região crítica). No fim das contas, não se pode usar tabelas z durante a prova, então eu não chutaria nada, ou chutaria que é verdadeiro (rejeitou a hipótese nula antes, rejeitaria com mais convicção depois).

Discussão posterior

De fato, o valor $\alpha$ que poderia fazer com que $\bar{X}=110$ passasse a ser aceito na hipótese nula (olhando somente para a cauda direita) deveria ser tal que $RC=[110,\infty )$, i.e. que a probabilidade de tipo de erro I seja³

$$\alpha =P\left(\bar{X}>110\mid H_0\right)=P\left(Z>2.5\right)$$

ou seja, $\alpha \approx 6$%⁴.

---

References

• BUSSAB, Wilton; MORETTIN, Pedro. Estatística básica. 2010.

Footnotes

1. Por serem mais extremos, i.e. estão nas caudas da distribuição. ↩

2. Estimada, pois, por hipótese, não se tem a variância de facto. ↩

3. Esse $\alpha$ é, de fato, o p-valor de $\bar{X}=110$. ↩

4. O nível de significância é a área das caudas da distribuição da hipótese nula. Ou seja, quanto menor for, mais amplo será o intervalo de confiança da hipótese nula; obviamente, ao se adotar essa visão mais “oblivious”, pode-se incorrer mais frequentemente em Erro do Tipo II $\beta$. ↩